There are several ways to find the equation of the line which passes through two points. The one I like the most is the vectorial method.
Let #v# be the vector that connects two points #P_0=(x_0,y_0)# and #P_1=(x_1,y_1)# and #k# a scalar, we can find any generic point #P=(x,y)# in their line by adding #k*v# to the coordinates of #P_0#.
#P = P_0 + k*v -> (x,y) = (x_0,y_0) + k*v#
#v = (x_1-x_0,y_1-y_0)#
#x = x_0 + k*(x_1-x_0) -> k = ((x-x_0))/((x_1-x_0))#
#y = y_0 + k*(y_1-y_0) -> k = ((y-y_0))/((y_1-y_0))#
#((x-x_0))/((x_1-x_0)) = ((y-y_0))/((y_1-y_0))#
#y = (x-x_0)*((y_1-y_0))/((x_1-x_0))#//
Hope it helps.
Or
1) Find the slope using ...
#m=(y_2-y_1)/(x_2-x_1)=(1-3)/(8-(-2))=(-2)/(8+2)=(-2)/10=-1/5#
2) Find the #y#-intercept, #b#, by using the slope intercept equation, #y=mx+b#
Use either of the points. I will use the #(8,1)#.
#1=(-1/5)(8)+b#
#1=(-8/5)+b#
#1+(8/5)=b#
#5/5+(8/5)=b#
#13/5=b#
3) Rewrite the slope intercept form, #y=mx+b#, and substitute in the #y#-intercept, #b#, and the slope, #m#.
#y=-1/5x+13/5#
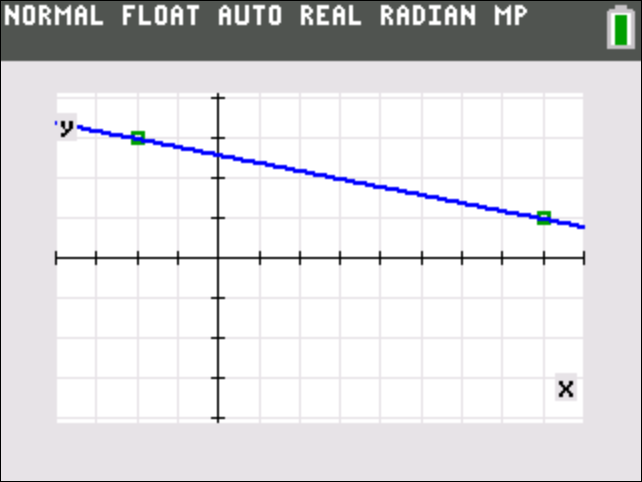
In the image below see the function graphed. The green squares are the points (8,1) and (-2,3). Notice that they are on the line.