Question

How do I find the horizontal limits of f(x)=(2x^3-11x^2-11x)/(5-9x-6x^3)?

I'm not entirely sure what it is wanting me to do. There doesn't seem to be much to factor other than the x out of the top part. What exactly do I do to find horizontal limits?

Answer 1

See below.

Explanation:

The question is really asking you to find the limit to infinity. This is sometimes called the end behaviour of a polynomial. When we have rational functions like the one given, the limit to infinity will tend towards a horizontal line, unless the degree of the numerator is higher than the degree of the denominator, in which case it tends towards an oblique asymptote. To find this, we only need to concentrate on the terms of the highest degree in the numerator and denominator.

These terms increase more rapidly than the terms of lower degree.

From the given function we have:

`(2x^3)/(-6x^3)`

This cancels to:

`-1/3`

So the limit to infinity is:

`lim_(x->+-oo)(2x^3-11x^2-11x)/(5-9x-6x^3)=-1/3`

This means as `x->+-oo` `\ \ \ \ \ \ \ f(x)->-1/3`

This is the horizontal asymptote:

`y=-1/3`

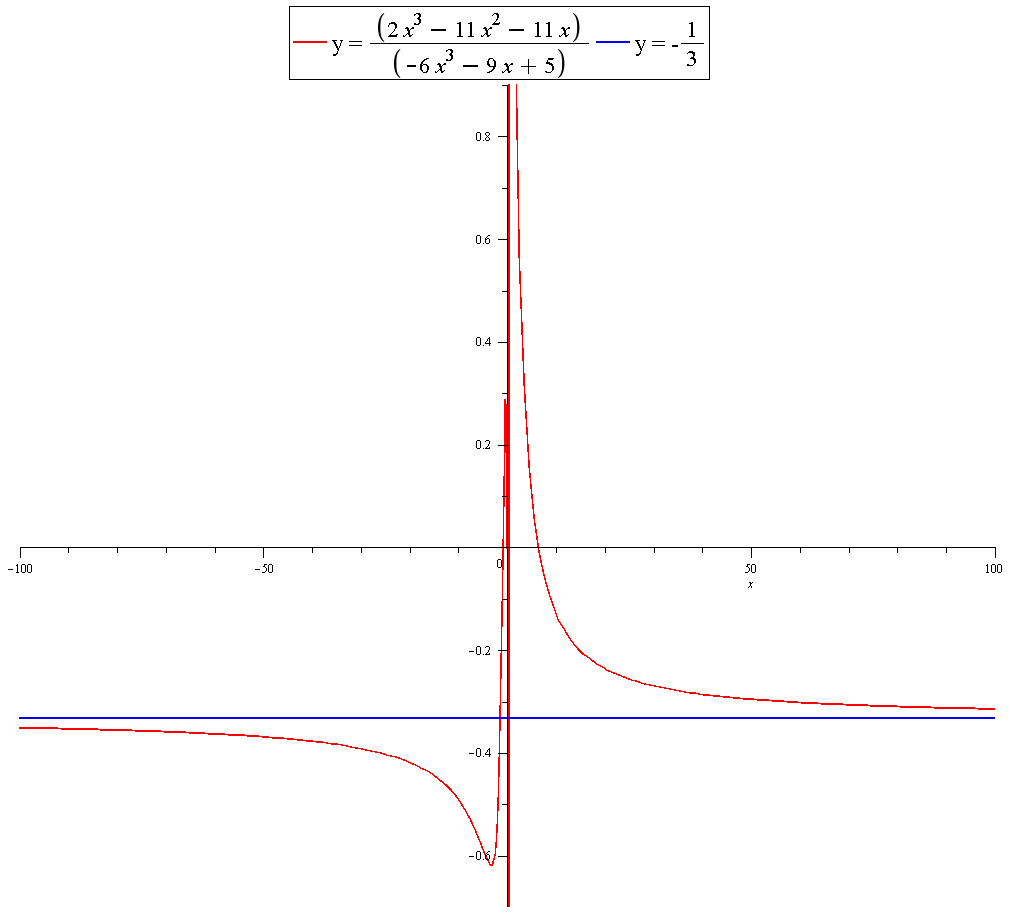
The graph confirms this: