How do I find the volume of the solid generated by revolving the region bounded by y=x^2, y=0, and x=2 about the x-axis? The y-axis?
1 Answer
May 19, 2018
1)
2)
Explanation:
the rose region is revolving about the x-axis and y-axis
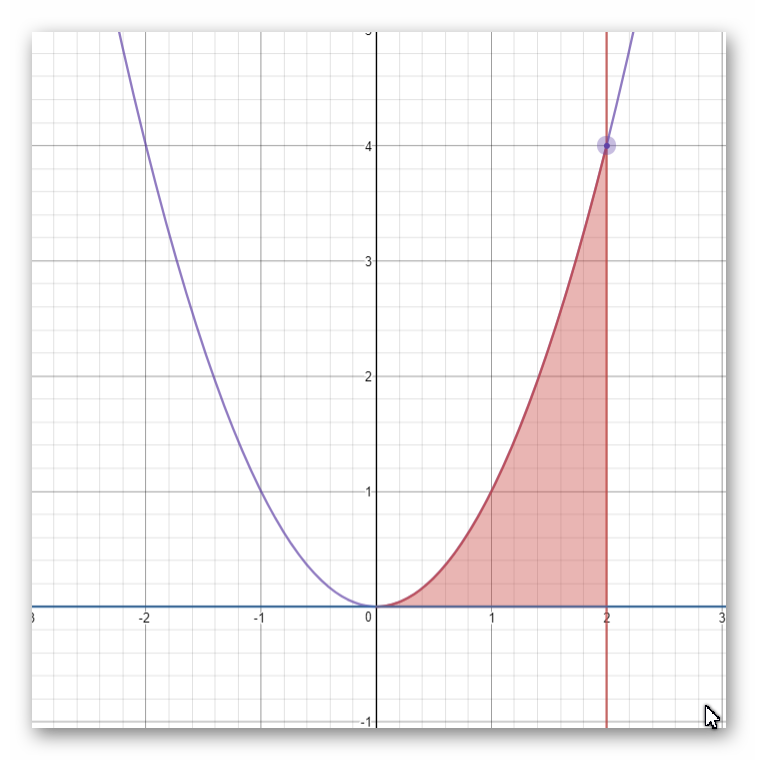 Desmos.com
Desmos.com
1)when the shaded region revolving a bout x-axis
2)when the shaded region revolving about the y-axis

