How do I multiply 3cis(pi/4) and 5cis(5pi/6)?

I'm not sure how to answer this question.

Multiply #3cis(pi/3) and 5cis((5pi)/6)#.

The answer I get is #15cis((7pi)/6)# but the argument has to be #-pi < arg(z) <= pi#.

How do I change the argument to keep it within the restrictions?

Please help!
Thank you :)

2 Answers
Narad T.
Mar 19, 2018

The answer is #=15cis(-11/12pi)#

Explanation:

In your calculations, you took #1/3pi# instead of #1/4pi#

Reminder

#e^axxe^b=e ^(a+b)#

By definition, and by Euler's relation

#cistheta=costheta+isintheta= e^(itheta)#

Therefore,

#3cis(1/4pi)=3e^(ipi/4)#

and

#5cis(5/6pi)=5e^(i5/6pi)#

So,

#3cis(1/4pi)xx5cis(5/6pi)=3e^(ipi/4)xx5e^(i5/6pi)#

#=15e^(i(pi/4+5/6pi))#

#=15e^(i(6/24pi+20/24pi))#

#=15e^(i(13/12pi))#

#=15cis(13/12pi)#

#=15cis(-11/12pi)#

as

#13/12pi=-11/12pi#

Make a drawing on the unit circle

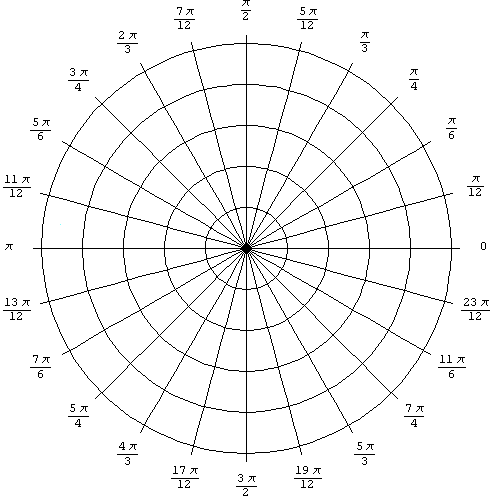
crewtonramoneshouseofmath.blogspot.com

Jim G.
Mar 19, 2018

#"see explanation"#

Explanation:

#"Given "z_1=r_1(costheta_1+isintheta_1)" and"#

#z_2=r_2(costheta_2+isintheta_2)#

#z_1z_2=r_1r_2(cos(theta_1+theta_2)+isin(theta_1+theta_2))#

#rArr3cis(pi/4)xx5cis((5pi)/6)#

#=15cis(pi/4+(5pi)/6)#

#=15cis((13pi)/12)#

#-pi< theta<=pi#

#((13pi)/12)"has related acute angle "(pi/12)#

#rArr-pi+pi/12=-(11pi)/12to(-pi< theta<=pi)#

#rArr15(cos((-11pi)/12)+isin((-11pi)/12))#

#["note that "cos(-x)=cosx" and "sin(-x)=-sinx]#

#=15(cos((111pi)/12)-isin((11pi)/12))#

Related questions
Impact of this question
3175 views around the world
You can reuse this answer
Creative Commons License