Question

How do I calculate the Fourier Transform of `a/(2pi) 1/(a^2 + x^2)`?

Define `mathcal(F)_(omega)[f(x)] = hat(f)(omega)` as the Fourier transform of `f(x)`:

`hat(f)(omega) -= mathcal(F)_(omega)[f(x)] = 1/(sqrt(2pi)) int_(-oo)^(oo) f(x)e^(-iomegax)dx`

and define the inverse Fourier transform `mathcal(F)_(x)^(-1)[hat(f)(omega)]` of `hat(f)(omega)` as:

`f(x) -= mathcal(F)_(x)^(-1)[hat(f)(omega)] = 1/(sqrt(2pi)) int_(-oo)^(oo) hat(f)(omega) e^(iomegax)dx`

How would I evaluate a Fourier Transform with:

`f(x) = a/(2pi) 1/(a^2 + x^2)`?

Answer 1

`int_(-oo)^(oo) \ e^(i omega x )/(a^2+x^2) \ dx = (pi e^(-omega a ))/(a)`

Explanation:

I never studied Fourier Transforms, but at the end of the day it is just an integral transform similar to Laplace, so:

I won't worry about the `a/(2pi)` weight of the function or the `1/sqrt(2pi)` weight of the transform, and just calculate

`I_x = int_(-oo)^(oo) \ e^(i omega x )/(a^2+x^2) \ dx` where `x in RR`.

In order to compute this definite integral, consider the following complex variable function over a domain `CC`:

`f(z) = e^(i omega z )/(a^2+z^2)`

And its associated contour integral:

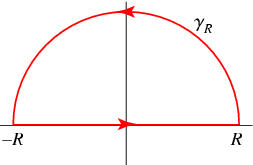
`I_z = oint_C \ f(z) \ dz`

Where `C` is the following semi-circular contour in the complex plane with radius `R gt 0`:

We will restrict `R` to enclose the poles in the upper quadrants once we have analyzed the poles of `f(z)`. The denominator of the integrand is `a^2+z^2`, and so we have simples poles when `z^2+a^2 = 0 => z=+-ai`.

We need only be concerned with the poles in Q1 and Q2, that (providing we make `R` large enough) lie within our contour `C`, that is the pole `z=ai`, assuming that `a` is positive.

So then:

`oint_C \ f(z) \ dz = int_(-R)^(R) \ f(x) \ dx + int_(gamma_R) \ f(z) \ dz`

As `C` encloses a single pole:

`alpha = ai` (assuming `a gt 0`)

Then by the residue theorem:

`oint_C \ f(z) \ dz = 2pii xx ( ("sum of the residues of the"), ("poles of " f(z) " within "C) )`
`" " = 2pii \ { res_(z=alpha) \ f(z)`

And we can calculate the residues as follows:

`res_(z=alpha) = lim_(z rarr alpha) (z-alpha) f(z)`
`" " = lim_(z rarr ai) (z-ai) ( e^(i omega z )/(a^2+z^2) )`
`" " = lim_(z rarr ai) (z-ai) ( e^(i omega z )/((z-ai)(z+ai)) )`
`" " = lim_(z rarr ai) ( e^(i omega z )/(z+ai) )`
`" " = e^(i omega ai )/(ai+ai)`
`" " = e^(-omega a )/(2ai)`

Thus:

`oint_C \ f(z) \ dz = 2pii e^(-omega a )/(2ai) = (pi e^(-omega a ))/(a)`

Now, as we let `R rarr oo` we get:

`oint_C \ f(z) \ dz = int_(-oo)^(oo) \ f(x) \ dx + int_(gamma_R) \ f(z) \ dz`

As is often the case with contour integrals, we find that:

`lim_(R rarr oo) int_(gamma_R) \ f(z) \ dz = 0`

So we will end up with the result:

`int_(-oo)^(oo) \ e^(i omega x )/(a^2+x^2) \ dx = oint_C \ f(z) \ dz`
`" " = (pi e^(-omega a ))/(a)`