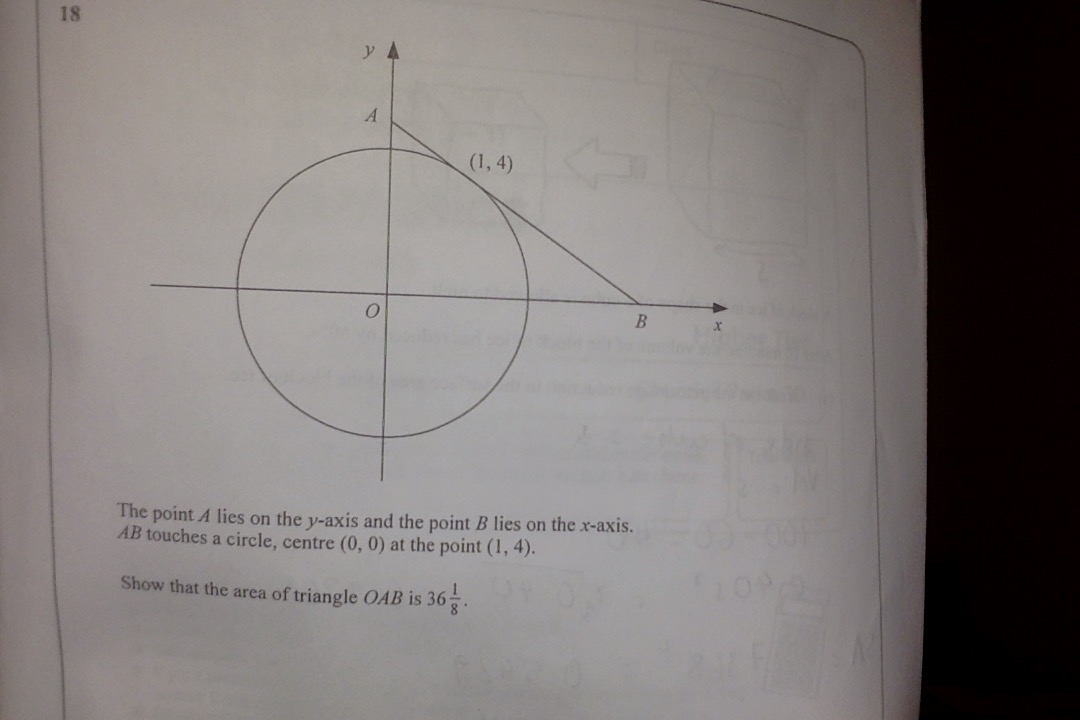
How do I show that the area of the triangle OAB is 36 1/8 ?
3 Answers
Explanation:
#"area of "triangleOAB=1/2xx"base"xx"height"#
#color(white)(xxxxxxxxxxx)=1/2xxOBxxOA#
#"we require to find the coordinates of A and B"#
#"obtain the equation of the tangent line AB"#
#"remembering that the tangent is at right angles to"#
#"the radius"#
#"the slope of the radius between" (0,0)" and "(1,4)" is"#
#m_("radius")=(Deltay)/(Deltax)=4/1=4#
#"hence the slope of the tangent line is"#
#m_("tangent")=-1/m=-1/4#
#rArry=-1/4x+blarrcolor(blue)"is the partial equation"#
#"to find b substitute "(1,4)" into the partial equation"#
#4=-1/4+brArrb=4+1/4=17/4#
#rArry=-1/4x+17/4larrcolor(red)"equation of tangent line"#
#x=0rArry=17/4rArrA=(0,17/4)#
#y=0rArr-1/4x+17/4=0rArrx=17rArrB=(17,0)#
#"area of "triangleOAB=1/2xx17xx17/4#
#color(white)(xxxxxxxxxxxx)=289/8=36 1/8" units"^2#
Please refer to the Explanation.
Explanation:
Name the point of contact
Let,
Since,
Clearly, the eqn. of
Recall that, the eqn. of tgt.
Hence,
This eqn. of
See the explanation below.
Explanation:
Let point C(1, 4) be the point of tangency then the radius OC:
The OC is also perpendicular to AB, draw two lines from C perpendicular to OB and OA at points D and and E respectively:
We can calculate the following angles:
OAD = arctan(1/4)=14 degrees
OCE = 90 - 14 = 76 degrees
Now consider two right triangles AEC and DCB:
Angle EAC and DCB are equal also angles ECA and DBC are equal, we can calculate the following angles:
EAC = DCB = 90 - 14 = 76 degrees
ECB = DBC = 90 - 76 = 14 degrees
We can calculate the following lengths:
then:
Finally the area of OAB is:

