Question

How do I solve this equation? `tan^2(x)+tan(x)-1= tan(x)`

Answer 1

`x=pi/4+npi`

`x=(3pi)/4+npi`

Explanation:

Move all tangents to the same side, yielding

`tan^2x+cancel(tanx-tanx)-1=0`

`tan^2x-1=0`

We can factor this using the Difference of Squares, which tells us

`x^2-a^2=(x+a)(x-a)`

Thus, `tan^2x-1=(tanx+1)(tanx-1)` and we're left with

`(tanx+1)(tanx-1)=0`

The solutions are then

`tanx=-1`
`tanx=1`

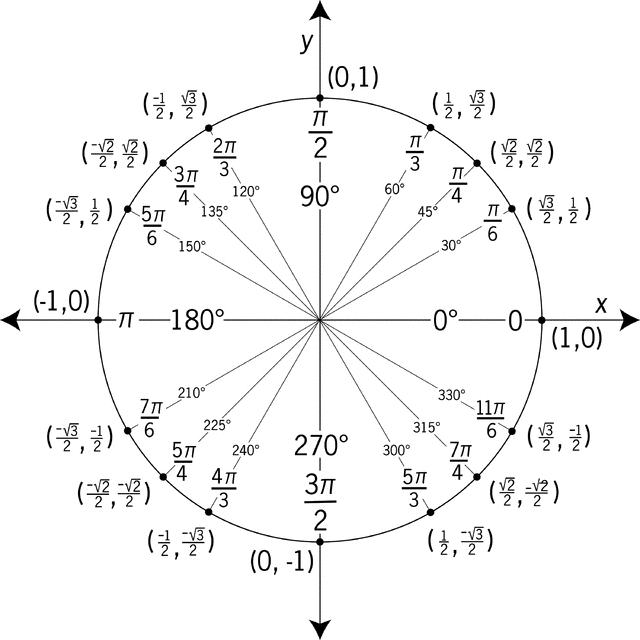
Examining the unit circle, we see that the values of `x` which yield a positive or negative one for `tanx,` or `sinx/cosx`, are `x=pi/4, (3pi)/4, (5pi)/4, (7pi)/4`. Sine and cosine are either equal or equal in everything but sign at these values; since tangent is sine divided by cosine, it must be equal to one at these points.

However, recall that tangent is periodic, all values for tangent repeat every `pi` units. We can account for all these other solutions by adding `pin` to the initially found solutions, where `n` is any integer.

So, we're left with

`x=pi/4+npi`

`x=(3pi)/4+npi`

`x=(5pi)/4+npi`

`x=(7pi)/4+npi`

We can omit the final two solutions, as the first two solutions actually encompass those since `pi` is always being added to them.

`x=pi/4+npi`

`x=(3pi)/4+npi`

Answer 2

Given: `tan^2(x)+tan(x)-1= tan(x)`

Subtract `tan(x)` from both sides:

`tan^2(x)-1= 0`

Add 1 to both sides:

`tan^2(x)=1`

Take the square root of both sides:

`tan(x)=+-sqrt1 = +-1`

This separates into two equations:

`tan(x) = -1` and `tan(x) = 1`

`x = pi/4` and `x = -pi/4`

To describe all of the possible values of x, we need to add integer multiples of `pi` to both equations:

`x = pi/4+npi` and `x = -pi/4+npi` where `n in ZZ`