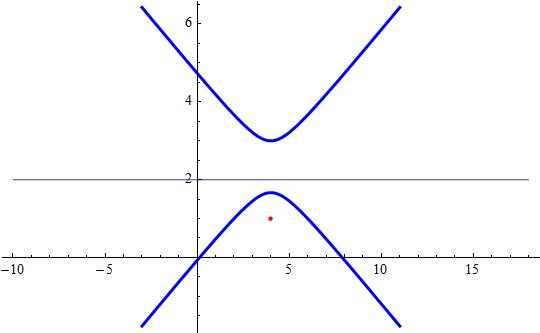
Give an equation to describe the locus of points P(x,y) where the distance of P from point A(4,1) is twice the distance of P from the line y=2?
Give an equation to describe the locus of points P(x,y) where the distance of P from point A(4,1) is twice the distance of P from the line y=2?
Give an equation to describe the locus of points P(x,y) where the distance of P from point A(4,1) is twice the distance of P from the line y=2?
1 Answer
May 2, 2017
Explanation:
Calling
Simplifying
The locus presents two leafs given by