How do I use long division to simplify #(2x^3+4x^2-5)/(x+3)#?
1 Answer
Hey! Long division is a fun topic once you get the hang of it! Don't be intimidated by the long answer, I just want to make sure you understand every step!
First thing you want to do is write the expression in long division form like so: 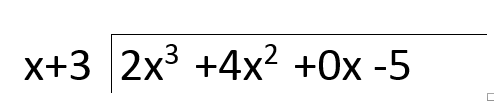
Notice how there is a 0x? If you don't already know, you have to add what is called a "place holder" if your exponents don't decrease until 1. In this case, you were missing the x^1.
Next, you look to see how many times "x" (on the left) can go into 2x^3. In essence, you are dividing 2x^3 by x. This results in 2x^2. With this answer, you place it in the x^2 column like so: 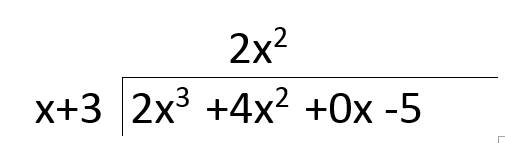
With this, you take what you just placed on top (2x^2) and multiply it by everything on the left, write a subtraction sign below the first column, then place the answer you got in brackets under the first two columns. After you've done this, do the subtraction, then bring whatever is left DOWN, like so:
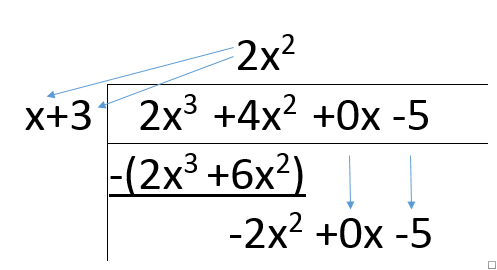
Notice how the 2x^3 gets cancelled out? Your leading term should get cancelled out each time you do this step, and the next ones!
Again, you check to see how many times "x" can go into -2x^2 (divide -2x^2 by x) and you should get -2x. So, take this and write it in the "x" column like so: 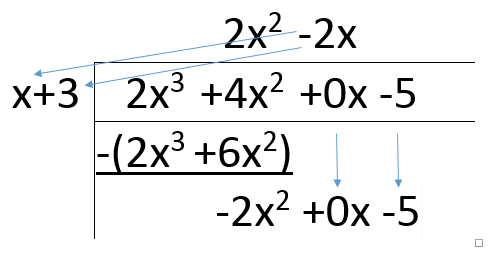
Now, like before, multiply the new term at the top by everything on the left, write a subtraction sign slightly to the left of the previous answer (-2x^2+0x-5) and write your new answer in brackets. Finally, do the math and bring the left over term (-5) DOWN!
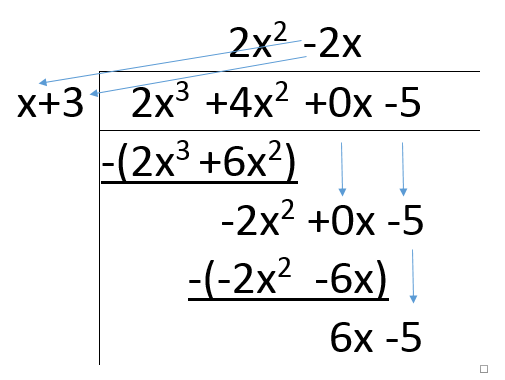
Now, determine how many times x goes into 6x (divide 6x by x), you should get 6. Write this in the "constants" (numbers without variable) column, multiply it by everything on the left, write a subtraction sign, put your new answer in brackets, then do the math! :)
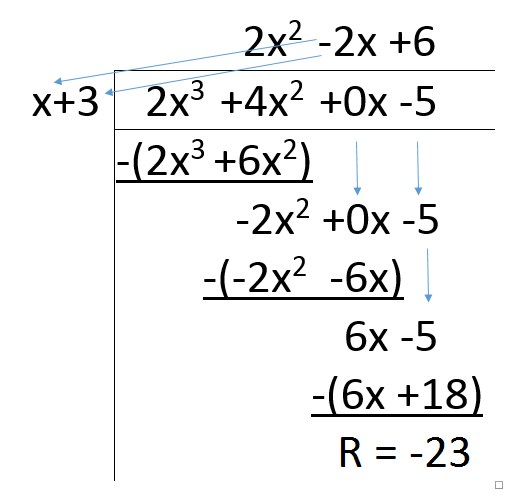
Your final answer should be 2x^2-2x+6 with a remainder of -23! However, your answer should be formatted like this:
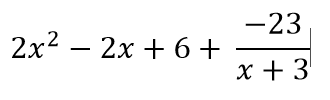
Your final answer will be on the left, then you ADD your REMAINDER OVER WHATEVER YOU WERE DIVIDING BY!
Hope this helps! Sorry for such a long explanation! :)

