Question

How do Wien's law and the Stefan-Boltzmann law describe blackbody radiation?

Answer 1

These two describe everything about a black body provided, we also know that the emission profiles of all black body is a Planck's Curve.

()

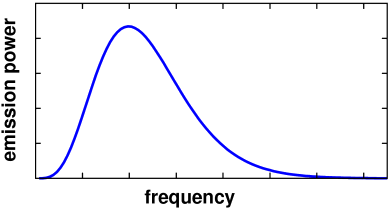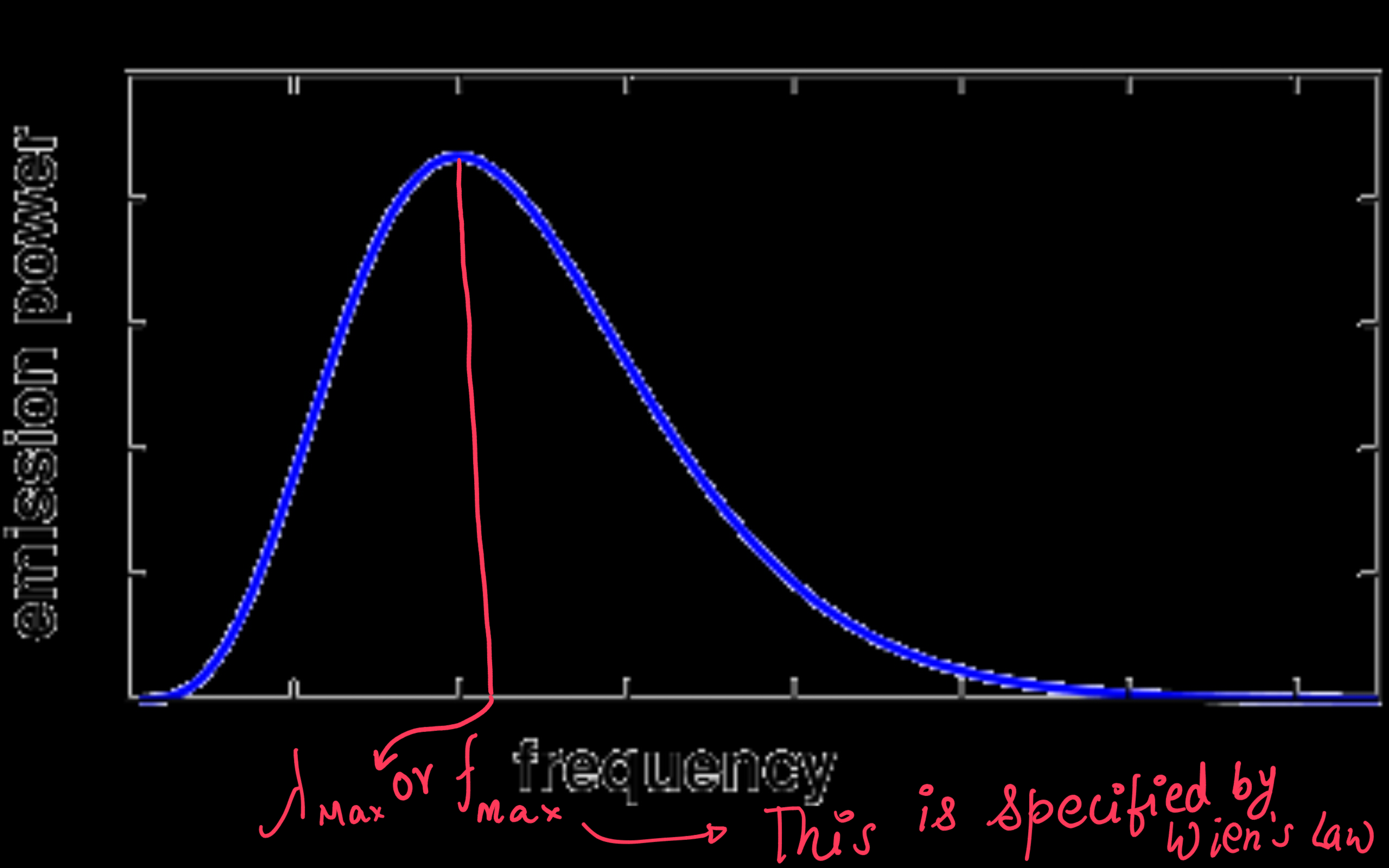
Wien's Law
Wein law states that the product of the equilibrium temperature of the black body and the wavelength which emits maximum power at that temperature is a constant.
or
`lambda xx T = b`

Now using Wien's Law one is able to find out the wavelength at which maximum power contribution exsists.

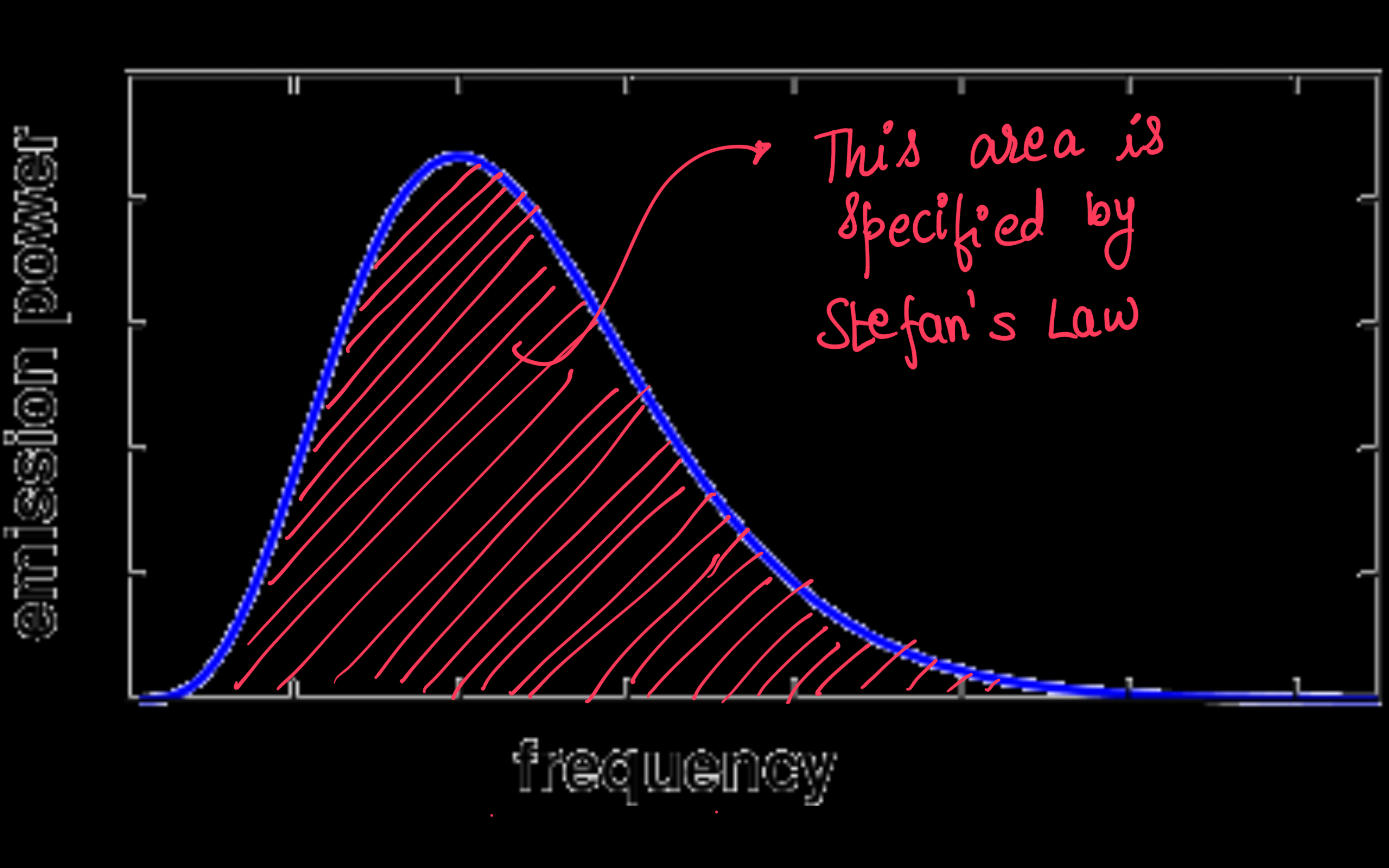
Stefan-Boltzmann's Law
Stefan-Boltzmann's Law states that the total power emitted by a black body due to all wavelengths is directly proportional to `T^4` and to the area of the black body
U= `sigma xx A xx T^4`
So what this essentially tells us mathematically is the area under the plank's curve of the given black body at a given temperature.

The last and final thing we need to realise is that a Planck's curve for a body at a given thermal equilibrium completely describes the black bodyMy explanation till now was to relate Planck's curve with Stefan's and Wien's Law. Now that we have done that we can move onto to answer the question.

A Planck's Curve can be completely constructed when `lambda_max` and area under the graph is given. Because `lambda_max` tells us where the curve peaks and U tells us how much area is enclosed by the curve. Just as a Normal distribution is completely described by its mean and variance, a Planck's Curve can be completely described by the wavelength(or frequency) at which it peaks and how much area it encloses. And Stefan's Law and Wien's Law provide us just that but these are only parts of the bigger picture which the Planck's Curve provides