An osmole (Osmol) is 1 mol of particles that contribute to the osmotic pressure of a solution.
For example, #"NaCl"# dissociates completely in water to form #"Na"^+# ions and #"Cl"^-# ions.
Thus, each mole of #"NaCl"# becomes two osmoles in solution: one mole of #"Na"^+# and one mole of #"Cl"^-"#.
A solution of 1 mol/L #"NaCl"# has an osmolarity of 2 Osmol/L.
A solution of 1 mol/L #"CaCl"_2# has an osmolarity of 3 Osmol/L (1 mol #"Ca"^(2+)# and 2 mol #"Cl"^-#).
EXAMPLE 1
Calculate the osmolarity of blood. The concentrations of solutes are:
#["Na"⁺] = "0.140 mol/L"#;
#"[Glucose]" = "180 mg/100 mL"#;
#"[BUN] (blood urea nitrogen)" = "20 mg/100 mL"#.
Solution
#"[Na"^+"]" = "0.140 mol/L"#.
But, each #"Na"^+# ion pairs with a negative ion #"X"^-# such as #"Cl"^-# to give 2 Osmol of particles.
#"NaX osmolarity" = (0.140cancel("mol"))/(1"L") × "2 Osmol"/(1cancel("mol")) = "0.280 Osmol/L"#
#"Glucose osmolarity" = (0.180 cancel("g"))/(100 cancel("mL")) × (1000 cancel("mL"))/"1 L" × (1 cancel("mol"))/(180.2 cancel("g")) × "1 Osmol"/(1 cancel("mol")) = "0.009 99 Osmol/L"#
#"BUN osmolarity" = (0.020 cancel("g"))/(100 cancel("mL")) × (1000 cancel("mL"))/"1 L" × (1cancel("mol"))/(28.01 cancel("g")) ×"1 Osmol"/(1cancel("mol")) = "0.0071 Osmol/L"#
#"Blood osmolarity" = "(0.280 + 0.009 99 + 0.0071) Osmol/L"= "0.297 Osmol/L" = "297 mOsmol/L"#
EXAMPLE 2
Calculate the osmolarity of an IV admixture that contains 500 mL sterile water; 50 mL NaHCO₃ 8.4 %; 10 mL of 2 mmol/mL KCl; 0.5 mL heparin 5000 units; 1 mL pyridoxine; 1 mL thiamine.
Solution
Set up a table for easy calculation.
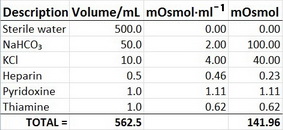
#"Osmolarity" = "141.96 mOsmol"/(562.5 cancel("mL")) × (1000 cancel("mL"))/"1 L" = "252 mOsmol/L"#



