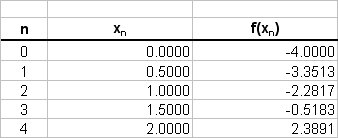
How do you calculate the left and right Riemann sum for the given function over the interval [0,2], n=4 for # f(x) = (e^x) − 5#?
1 Answer
# L RS = -5.0757#
# R RS = -1.8811 #
Explanation:
We have:
# f(x) = e^x-5 #
graph{e^x-5 [-10, 10, -8, 8]}
We want to calculate over the interval
# Deltax = (2-0)/4 = 1/2#
Note that we have a fixed interval (strictly speaking a Riemann sum can have a varying sized partition width). The values of the function are tabulated as follows;
Left Riemann Sum
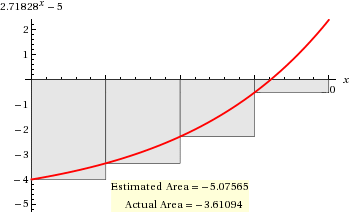
# L RS = sum_(r=0)^3 f(x_i)Deltax_i #
# " " = 0.5 * (-4 - 3.3513 - 2.2817 - 0.5183) #
# " " = 0.5 * (-10.1513) #
# " " = -5.0757 #
Right Riemann Sum
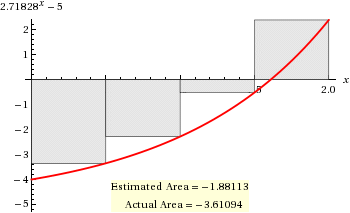
# R RS = sum_(r=1)^4 f(x_i)Deltax_i #
# " " = 0.5 * (-3.3513 - 2.2817 - 0.5183 + 2.3891) #
# " " = 0.5 * (-3.7623) #
# " " = -1.8811 #
Actual Value
For comparison of accuracy:
# Area = int_0^2 \ e^x-5 \ dx #
# " " = [e^x-5x]_0^2 #
# " " = (e^2-10) - (e^0-0) #
# " " = e^2-10 - 1#
# " " = e^2-11#
# " " = -3.610943 ...#