Question

How do you calculate the left Riemann sum for the given function over the interval [1,7], using n=3 for `(3 x^2+2 x +5)`?

Answer 1

588 (Using a right Riemann sum, oops)

Explanation:

I just realized the actual question was for a left Riemann sum, not a right one. Pardon my mistake. Below is the procedure for evaluating it with a right Riemann sum:

The general formula for a right-sided rectangle Riemann approximation on the interval `[a,b]` using `n` rectangles is:
`sum_(i=1)^n f(a+iDeltax)Deltax`
where `Deltax=(b-a)/n`

Plugging in the numbers, we get:
`Deltax=(7-1)/3=6/3=2`
`sum_(i=1)^3 2(3(1+2*i)^2+2(1+2*i)+5)`

We can multiply out the `2`:
`sum_(i=1)^3 6(1+2*i)^2+4(1+2*i)+10`

Now, let's evaluate it:
`6(1+2*1)^2+4(1+2*1)+10+6(1+2*2)^2+4(1+2*2)+10+6(1+2*3)^2+4(1+2*3)+10=`

`=6(3)^2+4(3)+10+6(5)^2+4(5)+10+6(7)^2+4(7)+10`

`=6*9+12+10+6*25+20+10+6*49+28+10`

`=588`

So, a `3`-part right-sided rectangle Riemann approximation on the interval `[1,7]` of `3x^2+2x+5` gives an area of `588`.

We can compare this to the actual answer, which would be computed using the anti-derivative:
`int_1^7 3x^2+2x+5=420`

If we look at the difference, we get `588-420=168`, which is an error of `40%`.

Answer 2

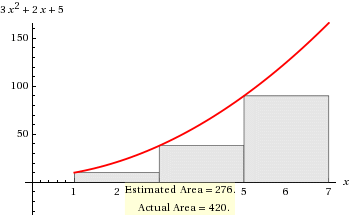
`LRS = 276`

Explanation:

Let:

`f(x) = 3x^2+2x+5`

We want to estimate `int \ f(x) \ dx` the interval `[1,7]` with `3` strips; thus:

`Deltax = (7-1)/3 = 2`

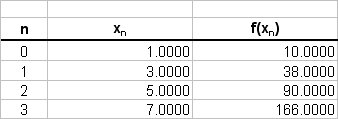
Note that we have a fixed interval (strictly speaking a Riemann sum can have a varying sized partition width). The values of the function are tabulated as follows;

Left Riemann Sum

`LRS = sum_(r=0)^2 f(x_i) \ Deltax_i`
`" " = 2 * (10 + 38 + 90)`
`" " = 2 * (138)`
`" " = 276`

Actual Value

For comparison of accuracy:

`Area = int_1^7 \ 3x^2+2x+5 \ dx`
`" " = [x^3+x^2+5x]_1^7`
`" " = (343+49+35) - (1+1+5)`
`" " = 427-7`
`" " = 420`