Question

How do you calculate the overlapping area between intersecting circles?

Answer 1

Calculate the area of the circular sector, from which subtract the area of the triangles whose base is the circles' chord defined by the intersection points; finally sum the results.

Explanation:

Consider Figs. 1 and 2

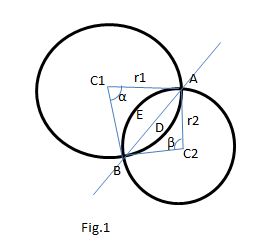
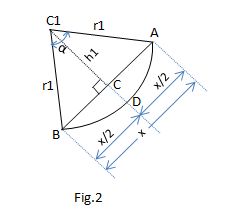
Figure 1 shows two circles (with centers `C1` and `C2` and radii `r_1` and `r_2`) that intercept each other in points A and B.

The area of interest is encompassed by arcs ADB and AEB.

In such a problem, most probably `r_1` and `r_2` are informed or aren't hard to find. This means that we can easily know the area of both the circles (as `pi*r_1^2` and `pi*r_2^2`).

We only need one more information to determine the area of the region ADBE: the proportion of any of the areas of circular sector to the total area of its circle or the angle of the circular sector (`alpha` or `beta`) or the length of the chord AB or even the coordinates of the center points `C1` and `C2`.

If we have the coordinates of the center points C1 and C2 as well as the radii `r_1` and `r_2`, we can obtain the circles' equations of whose conjugation we can obtain points A and B and therefore the length of the cord AB.

If we get the chord AB (called "x" in Figure 2 ) we can obtain `alpha` and `beta` in this way:
`tan (alpha/2)=(x/2)/r_1`
`tan (beta/2)=(x/2)/r_2`

Knowing `alpha` and `beta` we can determine the area of the circular sectors:
`S_("circular sector 1")=(alpha/360^@)*S_(circ_ 1)=(alpha/360^@)*pi*r_1^2`
`S_("circular sector 2")=(alpha/360^@)*S_(circ_ 2)=(alpha/360^@)*pi*r_2^2`

Next we can easily find `h_1` (height of `triangle_(ABC1)` in circle 1) and `h_2` (height of `triangle_(ABC2)` in circle 2).
Then with the chord AB (`=x`) as base and `h_1` or `h_2` as height we find the area of triangles ABC1 and ABC2.

Next we need just to subtract from each circular sector the area of its triangle.
Finally, we sum the results of the aforementioned subtractions obtaining the area of interest. Job done!

OR we could integrate the area between the equations of the two circles from the point A (`x_A, y_A`) to the point B (`x_B, y_B`).