How do you estimate the successive ionization energies of oxygen?
1 Answer
You go by oxygen's electron configuration.
Explanation:
LONG ANSWER
Ionization energy is simply the energy needed to remove one or more electrons from a mole of isolated atoms in gaseous state.
The ionization process produces positive ions, or cations.
The idea is that ionization energy depends on the magnitude of the attraction between the nucleus and the electrons. The more tighly held an electron is, the more energy will be needed to remove it from the atom.
The attraction between the nucleus and an electron that surrounds it depends on several factors
- the number of protons present in the nucleus;
- the distance between the nucleus and the electron;
- the amount of screening that exists for the electron.
Oxygen, which is located in group 16, period 2 of the periodic table, has an atomic number equal to 8 and a total of 8 electrons surrounding its nucleus.
Out of these 8 electrons, only 2 are considered core electrons, the rest being valence electrons.
This is important because the ionization energy for electrons located on the same energy level will be relatively similar in magnitude.
So, take a look at oxygen's electron configuration
The general idea is that the ionization energy will increase as you start removing electrons.
Despite the fact that all 6 valence electrons benefit from the same amount of screening from the two core electrons, the electron-electron repulsion that exists between them will impact the successive ionization energies.
As you remove electrons, this repulsion will decrease and the electrons will be harder to remove from the ion.
So, let's assume that you know oxygen's first ionization energy, which is equal to 1314 kJ/mol.
If you go by the above arguments, you can estimate that the second ionization energy will be similar in magnitude. The reduced repulsion means that you'll need more than 1314 kJ/mol to remove the second electron.
Let's say that you need 1,500 kJ/mol more for the second electron. This will get you
The third electron will require a little more energy, so I'll add an extra 1,750 kJ
The fourth will need a little more, so I'll add an extra 2,150 kJ
The fifth will need a little more, so I'll add an extra 2,900 kJ
The sixth will need a little more, so I'll add an extra 3,300 kJ
Now you're down to the last two electrons, the ones located in the first energy level.
To account for the fact that you now have to remove electrons that are both closer to the nucleus and that don't bebefit from any screening from the nucleus' pull, you need to drastically increase the ionization energies for these electrons.
Something like 50,000 kJ more for the seventh electron will do the trick. It doesn't have to be accurate, it just has to show that you understand the fact that these electrons will need more energy than the others.
The last electron will need a little extra, so something like 20,000 kJ more will work
Bottom line, don't worry about the exact values, focus on the trend.
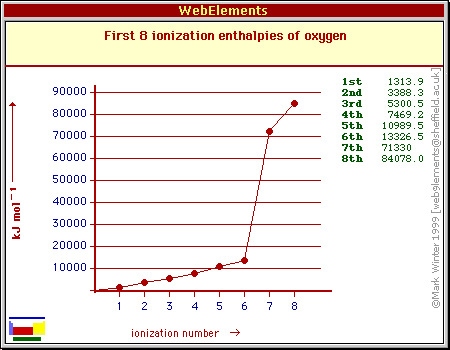
If you get the trend right, you can say that you estimated the successive ionization energies of oxygen correctly.

