Question

How do you calculate the total resistance in a parallel circuit?

Answer 1

`1/R_"eq" = 1/R_1 + 1/R_2`

Explanation:

I will assume that there are only 2 parallel resistors. After talking about that in some detail, I will briefly talk about many resistors in parallel.

If you put a voltage V across the 2 terminals leading to the pair of parallel resistors, both of them individually has the voltage V across it. See my sketch -- sorry for the poor photography.

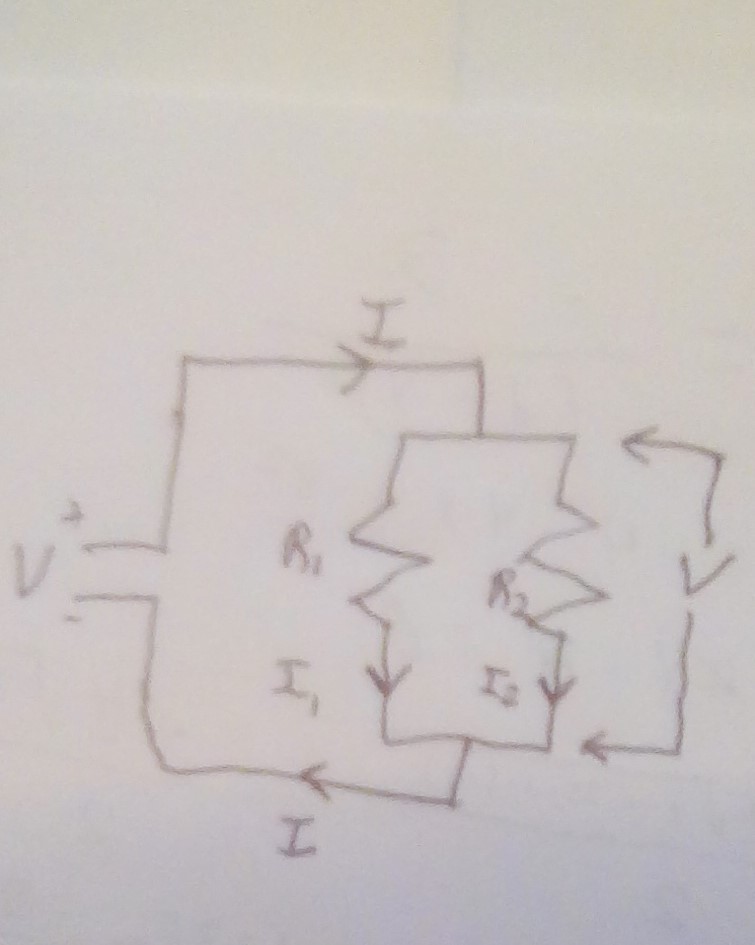
If you put a V in at the left, both `R_1 and R_2` have V volts across them. Therefore `I_1 and I_2` are as follows:

`I_1 = V/R_1 and I_2 = V/R_2`

The current out of the voltage source is the sum of those 2 currents.

`I = I_1 + I_2 = V/R_1 + V/R_2 = V*(1/R_1 + 1/R_2)`

Doing a bit more algebra on that,

`I = (V*R_2)/(R_1*R_2) + (V*R_1)/(R_2*R_1) = (V(R_1+R_2))/(R_1*R_2)`

Our goal is to find `R_"eq"` where we could write

`I = V/R_"eq"`.

So `R_"eq"` is the equivalent, or total, resistance of the circuit. Looking at the last 3 lines of math, we can say that

`1/R_"eq" = 1/R_1 + 1/R_2` Equation #1

Equation number 1 above may be in your textbook. Now, more algebra -- on Equation #1:

`1/R_"eq" = (R_1+R_2)/(R_1*R_2)` and

`R_"eq" = (R_1*R_2)/(R_1+R_2)` Equation #2

Once you have used Equation number 1 several times you may find number 2 more friendly. In industry it is called using "product over sum". It is to be used only for 2 resistors in parallel.

About situations with several resistors (any number of them) in parallel: an expansion of Equation #1

`1/R_"eq" = 1/R_1+1/R_2+1/R_3 + ... 1/R_n`

I hope this helps,
Steve