How do you calculating freezing point from molality?
1 Answer
One of the colligative properties of solutions is freezing-point depression.
This phenomenon helps explain why adding salt to an icy path melts the ice, or why seawater doesn't freeze at the normal freezing point of
The equation for freezing point depression is given by
#ulbar(|stackrel(" ")(" "DeltaT_f = imK_f" ")|)#
where
-
#DeltaT_f# represents the change in freezing point of the solution -
#i# is called the van't Hoff factor, which is essentially the number of dissolved particles per unit of solute (for example,#i = 3# for calcium chloride, because there is#1# #"Ca"^(2+) + 2# #"Cl"^(-)# ). -
#m# is the molality of the solution, the number of moles of solute dissolved per kilogram of solvent:
#"molality" = "mol solute"/"kg solvent"#
#K_f# is the molal freezing-point depression constant for the solvent, which the following table lists some values for certain solvents:
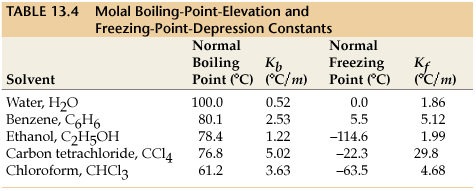
(the far-right column shows the
#K_f# )
Once you've calculated the change in freezing point, to find the new freezing point, you subtract the
#ul("new f.p." = "normal f.p." - DeltaT_f#
(I'd like to point out that depending on how you're taught, the

