How do you compare the graph of g(x) = x + 7 to the graph of f(x) = x?
1 Answer
Jan 4, 2018
As shown below...
Explanation:
For this problem we can first use our transformation knowledge, where if
So hence
We can also verify this by graphing the different lines, where we can tabualte a few values and draw the two lines...
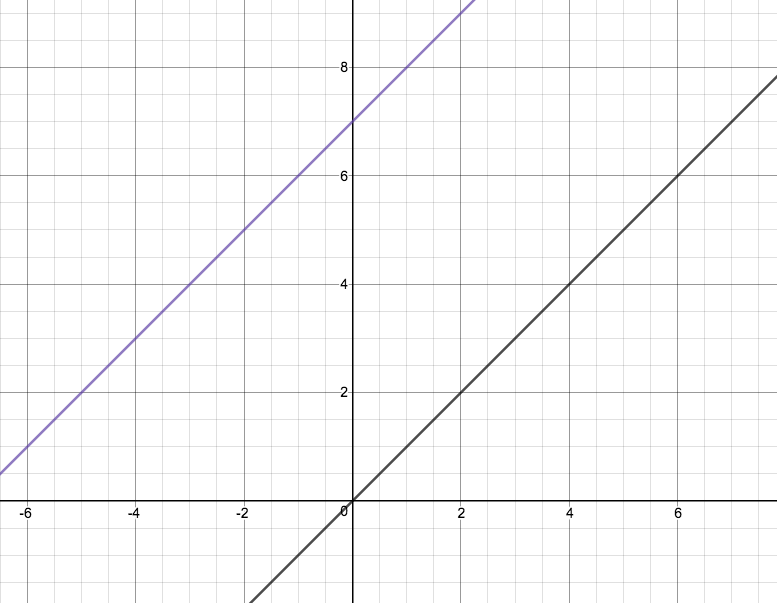
We can also see that the purple line,
Hence the two lines are also parrallel as they have the same gradient, and they never intersect...

