How do you compute the variance of the probability distribution in the table provided?

Question

Outcome | Probability
50 | 0.5
51 | 0.2
52 | 0.1
53 | 0.2?

29763 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-02-27T23:16:26

# Var(X) = 1.4#

Let #X# be the Random Variable that represents a possible outcome:

First we quickly check that #sumP(x) = 1# which is indeed the case.

The, we calculate #x^2#, #xP(x)#, and #x^2P(x)#:

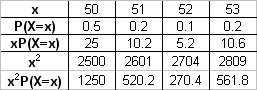
So then the Expectation is calculated using:

# E(X) = sum xP(x) #
# " " = 25+10.2+5.2+10.6 #
# " " = 51 #

Next prior to calculating the Variance we calculate E(X^2):

# E(X^2) = sum x^2P(x) #
# " " = 1250+520.2+270.4+561.8 #
# " " = 2602.4 #

Then we can calculate the variance:

# Var(X) = E(X^2) - E^2(X) #
# " " = 2602.4- (51)^2#
# " " = 2602.4- 2601#
# " " = 1.4#

We can also calculate the Standard Deviation (if required); as

# sigma^2 = Var(X) => sigma = 1.18 # (3sf)