How do you convert (-2, -2sqrt{3})(−2,−2√3)into polar coordinates?

1 Answer
Shantelle
May 5, 2018

(4, (4pi)/3)(4,4π3) (radians) or (4, 240^@)(4,240∘) (degrees)

Explanation:

Rectangular ->→ Polar: (x, y) -> (r, theta)(x,y)→(r,θ)

  • Find rr (radius) using r = sqrt(x^2 + y^2)r=√x2+y2
  • Find thetaθ by finding the reference angle: tantheta = y/xtanθ=yx and use this to find the angle in the correct quadrant

r = sqrt((-2)^2 + (-2sqrt3)^2)r=√(−2)2+(−2√3)2

r = sqrt(4+(4*3))r=√4+(4⋅3)

r = sqrt(4+12)r=√4+12

r = sqrt(16)r=√16

r = 4r=4

Now we find the value of thetaθ using tantheta = y/xtanθ=yx.

tantheta = (-2sqrt3)/-2tanθ=−2√3−2

tantheta = sqrt3tanθ=√3

theta = tan^-1(sqrt3)θ=tan−1(√3)

theta = (pi)/3θ=π3 or (4pi)/34π3

To determine which one it is, we have to look at our coordinate (-2, -2sqrt3)(−2,−2√3). First, let's graph it:
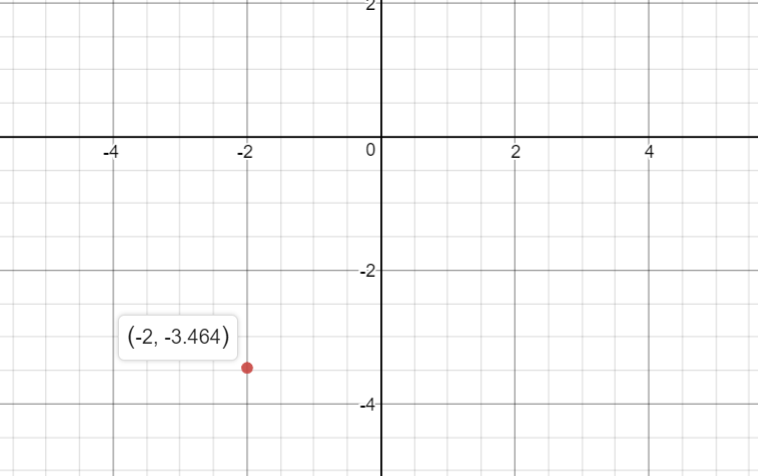
enter image source here

As you can see, it is in the third quadrant. Our thetaθ has to match that quadrant, meaning that theta = (4pi)/3θ=4π3.

From rr and thetaθ, we can write our polar coordinate:
(4, (4pi)/3)(4,4π3) (radians) or (4, 240^@)(4,240∘) (degrees)

Hope this helps!

Related questions
See all questions in Converting Coordinates from Rectangular to Polar
Impact of this question
24776 views around the world
You can reuse this answer
Creative Commons License