How do you convert from 300 degrees to radians?
1 Answer
To do this conversion you have to think at what is a radian.
A radian is the angle that describes an arc of length equal to the radius.
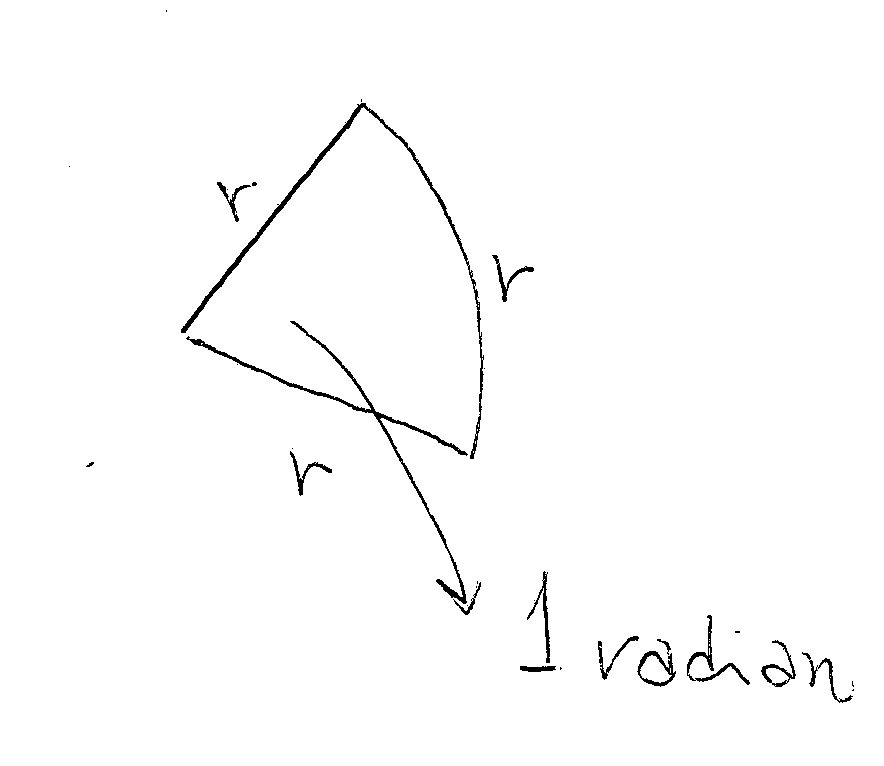
Figure 1
To make our life easier let us make
But what is the connection with degrees?
Consider an entire circle. We know that it spans 360° but how many radians?
If you try to draw them on top of your circle you'll find that you need a little bit more than 6 of the slices of figure 1 to cover your entire circle, i.e. 6 radians and a bit.
To get the exact number consider that an entire circle is a closed arc of length
Now we have the key for our conversion:
So:
if 360° is
if I have 300° I'll have
As a proportion:
and:
If you want you can multiply the value of
Hope it helps

