How do you convert $m^{3}$ $"m"^3$ to ${cm}^{3}$ $"cm"^3$ ?

Question

31634 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-07-11T20:24:43

${1 m}^{3} = 10^{6} {cm}^{3}$ $"1 m"^3 = 10^6"cm"^3$

All you need to know here is the following conversion factor

$color(purple)(|bar(ul(color(white)(a/a)color(black)("1 m" = 10^2"cm")color(white)(a/a)|)))$

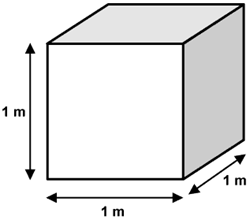
Now, a cubic meter can be thought of as the volume of a cube with a side of $"1 m"$ .

You can write the volume of the cube by raising the length of its side to the power of $3$

$"1 m"^3 = "1 m" xx "1m" xx "1 m"$

Notice that you can use the meter $->$ centimeter conversion factor to rewrite this as

$"1 m"^3 = overbrace(10^2"cm")^(color(blue)("= 1 m")) xx overbrace(10^2"cm")^(color(blue)("= 1 m")) xx overbrace(10^2"cm")^(color(blue)("= 1 m"))$

You will thus have

$"1 m"^3 = (10^2 xx 10^2 xx 10^2) ("cm" xx "cm" xx "cm")$

which gets you

$color(green)(|bar(ul(color(white)(a/a)color(black)("1 m"^3 = 10^6"cm"^3)color(white)(a/a)|)))$

How do you convert "m"^3m3"m"^3 to "cm"^3cm3"cm"^3?