How do you derive the area formula for a parallelogram?

1 Answer
sente
Dec 24, 2015

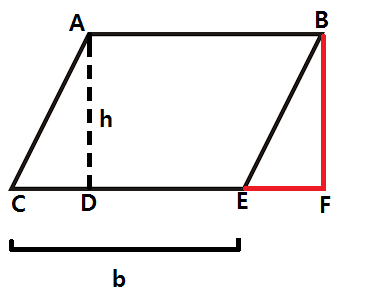
enter image source here

The intuition is fairly simple. In the above picture, we need to show that the area of parallelogram #ABEC# has the same area as the rectangle #ABFD#, which is #bh#.

Although it seems obvious from the picture, we cannot make the claim immediately without some justification. However, that justification comes fairly quickly when we show that triangles #ACD# and #BEF# are congruent.

To show that, we will use SSS congruence (two triangles with all three sides being equal are congruent). note that we immediately have #bar(AC) = bar(BE)# as opposite sides of parallelograms are equal and #bar(BF) = bar(AD)# by construction. Finally, to show that #bar(CD) = bar(EF)#, we first observe that #bar(CE) = bar(AB) = bar(DF)#, and therefore

#bar(CD) = bar(CE) - bar(DE) = bar(DF) - bar(DE) = bar(EF)#.

With that, we have #ACD ~= BEF#. Thus

#"area"(ABEC)="area"(ABED) + "area"(ACD)#

#="area"(ABED) + "area"(BEF)#

#="area"(ABFE)#

#=bh#

Related questions
See all questions in Perimeter and Area of Non-Standard Shapes
Impact of this question
9161 views around the world
You can reuse this answer
Creative Commons License