We have the series of sequence #u_n = n e^(-n/2)=n/sqrt(e^n)#.
In order to use the integral test, #f(n) = u_n# must be positive and decreasing on #[p;+oo[#.
Let's study the sign of #f(n)# :
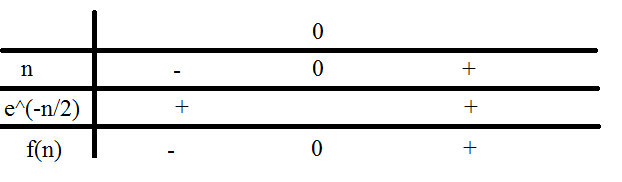
(Note : #e^(-n/2)# is always positive and it has the value of zero only if #n->+oo#; therefore, the sign of #f(n)# depends only on the numerator : #n#.)
Thus, #f(n)# is positive on #]0; +oo[#.
Let's study the slope (the growth) of #f(n)#, which comes down to study the sign of #f'(n)#.
The derivative of a function #f(x) = g(x)*h(x)# is :
#f'(x) = g'(x)h(x) + g(x)h'(x)#.
Therefore :
#f(n) = n * e^(-n/2) = g(n)*h(n)#
#f'(n) = (n)' * e^(-n/2) + n * (e^(-n/2))'#
#f'(n) = e^(-n/2) + n * (-n/2)' * (e^(-n/2))#
#f'(n) = e^(-n/2) + n * (-1/2) * (e^(-n/2))#
#f'(n) = e^(-n/2)*(1-n/2)#
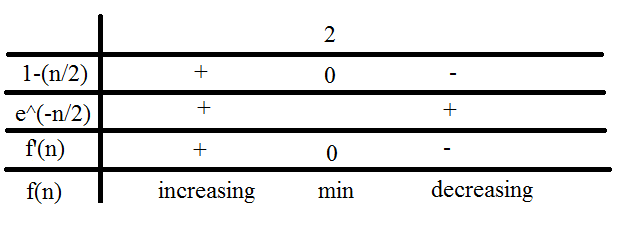
(Again, the sign of #f'(n)# depends only on the numerator : #1-n/2#).
Thus, #f(n)# is positive and decreasing on #[+2;+oo[#.
So we can use the integral test.
The series of sequence #u_n# converges if #int_p^(+oo) f(x) dx# exists.
Of course, here #f(x) = e^(-x/2) x# and #p = 2#.
If we want to calculate the integral, we must firstly find the antiderivative of #f(x)#.
The antiderivative of a function #f(x) = g'(x)h(x)# is :
#F(x) = g(x)h(x) - intg(x)h'(x)dx#
We have #f(x) = e^(-x/2) * x = g'(x) * h(x)#
We know that the derivative of #e^(-x/2)# is #-1/2e^(-x/2)#.
So we can easily find the antiderivative of #g'(x) = e^(-x/2)# :
#g(x) = -2*e^(-x/2)#.
So #F(x) = (-2*e^(-x/2)*x) - (int-2*e^(-x/2)*1)#
Again, we can easily find the antiderivative of #-2*e^(-x/2)#, which is #4*e^(-x/2)#.
#F(x) = (-2*e^(-x/2)*x) - (4*e^(-x/2)) = -2e^(-x/2)*(x+2) = -(2(x+2))/sqrt(e^x)#.
Therefore :
#int_p^(+oo) f(x) dx = [F(x)]_2^(+oo) = ''F(+oo)'' - F(2) = 0 +(2(2+2))/sqrt(e^2) = 8/e#.
(Note : #''F(+oo)'' = 0# since #sqrt(e^x)# increases faster to #+oo# than #x#).
Therefore, the series of sequence #u_n# is convergent.

