Question

How do you determine the limit of `4/(x-5)^2` as x approaches 5?

Answer 1

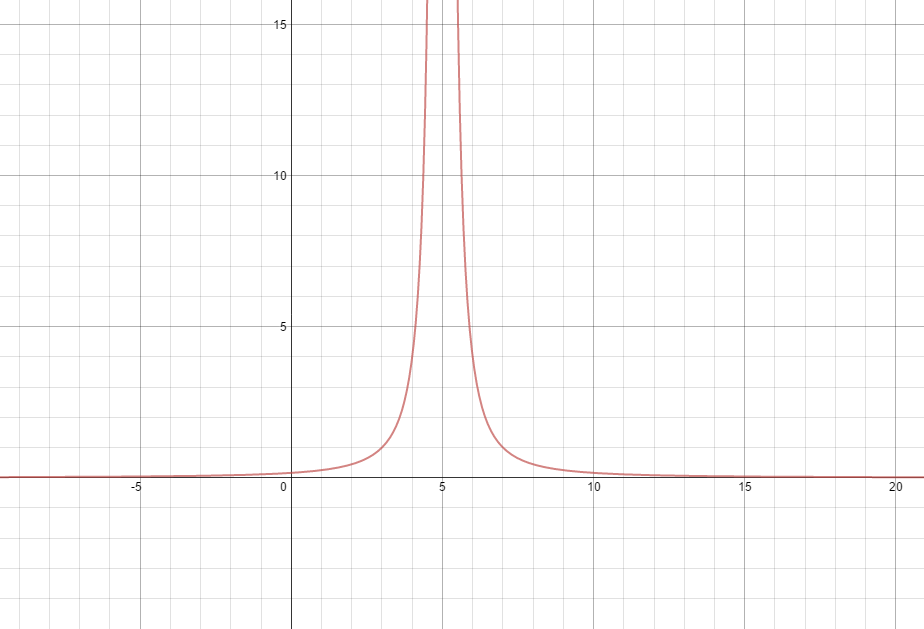
The limit `lim_(x->5) 4/(x-5)^2=1/0` which is an undefined form.This means that the limit does not exist there.

Taking side-limits we have that `lim_(x->5^+) 4/(x-5)^2=+oo` (values of x from the right of point `x=5`) and `lim_(x->5^-) 4/(x-5)^2=+oo` (values of x from the left of point `x=5`)

Since `4/(x-5)^2->+oo` increases without bound from both sides of point `x=5` we say that

`lim_(x->5) 4/(x-5)^2=+oo`

Note that this is not saying that the limit exists, since
`oo` is not a real number.

The graph of `4/(x-5)^2` around `x=5` explains visually our result.