Question

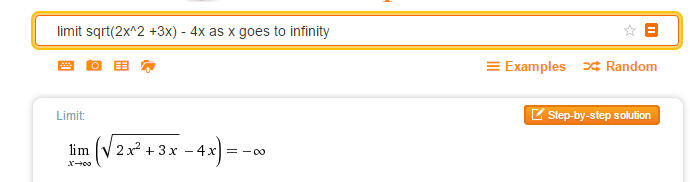
How do you determine the limit of `sqrt(2x^2 +3x) - 4x` as x approaches `oo`?

Answer 1

We have that

#sqrt(2x^2 +3x) - 4x=(sqrt(2x^2 +3x) - 4x)*(sqrt(2x^2 +3x) +4x)/(sqrt(2x^2 +3x) + 4x)= [(sqrt(2x^2+3x))^2-(4x)^2]/((sqrt(2x^2 +3x) + 4x))= (2x^2+3x-16x^2)/((sqrt(2x^2 +3x) + 4x))= (3x-14x^2)/[x(sqrt(2+3/x)+4))= x^2(3/x-14)/[x(sqrt(2+3/x)+4))= x(3/x-14)/[sqrt(2+3/x)+4] #

Hence the limit is

`lim_(x->oo) x*[3/x-14]/[sqrt(2+3/x)+4] =(oo) times [0-14]/(sqrt2+4)=-oo`

Footnote
WolframAlpha agrees with the above result as well