How do you determine the maximum height of a projectile?
1 Answer
You use the fact that the vertical component of the initial velocity is zero at maximum height.
Explanation:
When you launch a projectile at an angle
In order to determine the maximum height reached by the projectile during its flight, you need to take a look at the vertical component of its motion.
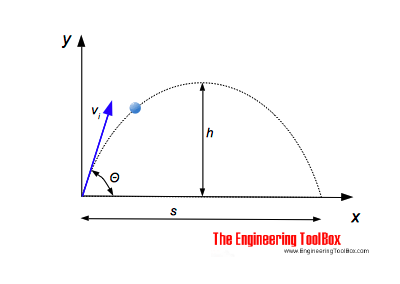
Vertically, the motion of the projectile is affected by gravity. This means that at maximum height, the vertical component of the initial speed will be zero.
The projectile will decelerate on its way to maximum height, come to a complete stop at maximum height, then starts its free fall descent towards the ground.
If you use the vertical component of its initial speed, you can write
This is equivalent to
The maximum height reached by the projectile will thus be

