This kind of problem is usually done with implicit differentiation. We begin by writing the function in terms of #x# and #y# as such:
#y = arctan(8^x)#
Next, we use the definition of #arctan# to rewrite the inverse in terms of the original #tan#:
#tan y = 8^x" " [A]#
We can now proceed with the implicit differentiation with respect to #x#:
#d/dx (tan y) = d/dx (8^x)#
#sec^2 y * dy/dx = 8^x (ln 8)#
#dy/dx = (8^x (ln 8))/(sec^2 y)#
#dy/dx = 8^x (ln 8) * (cos^2 y)" " [B]#
In line [B] we note that the definition of #sec y# is #1/(cos y)# and make the suitable substitution.
The issue with this is the derivative still contains a term of #y#, which we must remove. The clever trick here is to go back to line [A] in the solution and recognize that we can use the trigonometric definition of tangent to define a right triangle using this information:
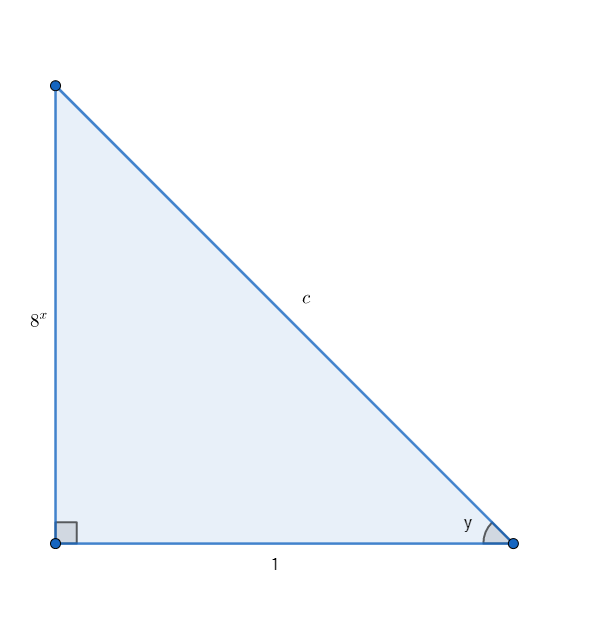
Note how the picture illustrates the fact that #tan y = 8^x = ("opposite")/("adjacent")# from trigonometry.
Using trigonometry, we can now evaluate what the value of #cos y# should be, and thus also #cos^2 y# which needs to be replaced in our form of the derivative. Note that #c# (the hypotenuse) can be derived from the Pythagorean Formula:
#c^2 = a^2 + b^2 #
#c^2 = (8^x)^2 + (1^2) #
#c^2 = 8^(2x) + 1 #
Thus:
#cos y = ("adjacent")/("hypotenuse") = 1/c #
#cos^2 y = (1 / c)^2 = 1 / c^2 = 1 / (8^(2x) + 1) #
Finally:
#dy/dx = 8^x (ln 8) * (cos^2 y) = 8^x (ln 8) * (1 / (8^(2x) + 1))#
# :. dy/dx = (8^x (ln 8)) / (8^(2x) + 1) #

