How do you divide #6x^3+5x^2-4x+4# by #2x+3#?

Question

1239 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-08-10T06:02:01

#(6x^3+5x^2-4x+4)/(2x+3) = 3x^2-2x+1+1/(2x+3)#

We can long divide the coefficients...

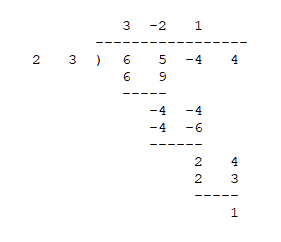
enter image source here

This tells us that #6x^3+5x^2-4x+4# divide by #2x+3# is #3x^2-2x+1# with remainder #1#

Equivalently, we can split off multiples of #2x+3# from #6x^3+5x^2-4x+4# as follows...

#6x^3+5x^2-4x+4#

#=6x^3+9x^2-4x^2-6x+2x+3+1#

#=3x^2(2x+3)-2x(2x+3)+1(2x+3)+1#

#=(3x^2-2x+1)(2x+3)+1#

So:

#(6x^3+5x^2-4x+4)/(2x+3) = 3x^2-2x+1+1/(2x+3)#