How do you divide #sqrt(12x^3y^12)/sqrt(27xy^2)#?
2 Answers
Mar 22, 2015
Take one big root to get:
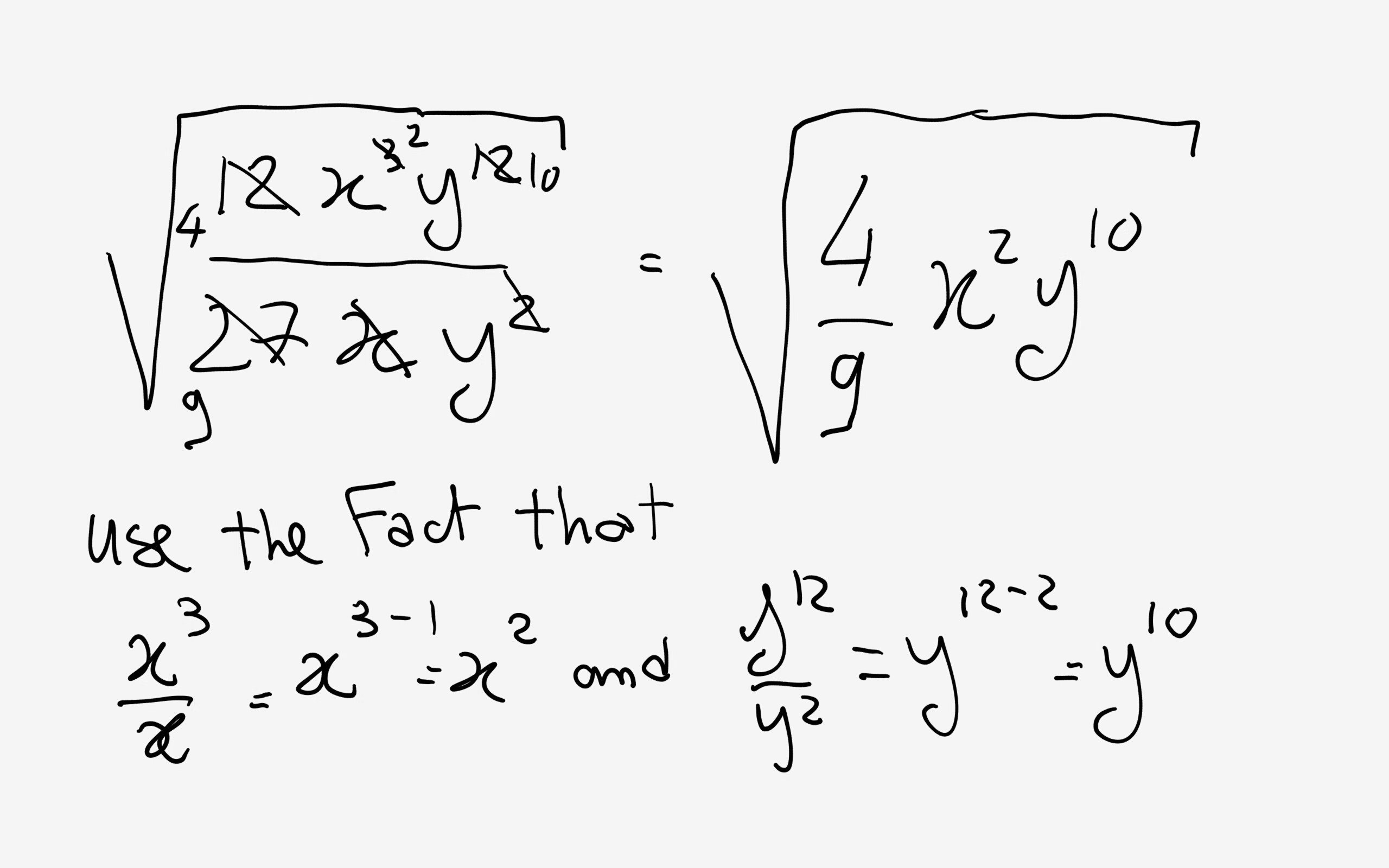
and finally taking the square root:
Hope it helps!
Mar 22, 2015
There are several good approaches to this question:
The reason I try this is that I see some common factors. Namely
Write it as a single square root, then simplify, the break it up into smaller square roots.
Or simplify both numerator and denominator, then simplify what you can.
Or:
(Rationalizing the denominator would work too, eventually.)


