Question

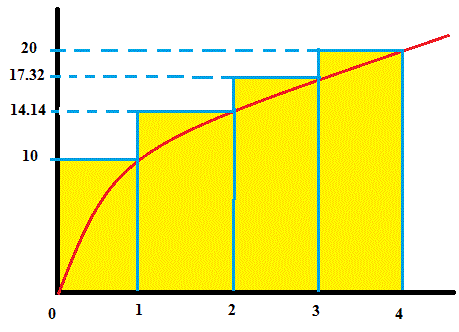
How do you estimate the area under the graph of `f(x) = 10sqrt(x)` from `x = 0` to `x = 4` using four approximating rectangles and right endpoints?

Answer 1

Using equal width rectangles, the 5 sides (remember you need 5 sides for 4 touching rectangles) will occur at
`x=0`, `x=1`, `x=2`, `x=4`, and `x=4`

The right endpoints of the rectangles will have heights"
`f(1) = 10`,
`f(2) = 10 sqrt(2) = 14.14` (approx.),
`f(3) = 10 sqrt(3) = 17.32` (approx.), and
`f(4) = 20`

Since each area has a width of `1` the total area of the `4` approximating rectangles is
`10 + 14.14 + 17.32 + 20`
`= 61.46`