How do you estimate the mean of a random walk?
1 Answer
You must apply the properties of expected values; e.g. if two variables are independent, the expected value of the sum is the sum of the expected values.
Explanation:
First of all we should be sure we are talking the same language. If so, this answer is valid, otherwise, the question must be reformulated.
Random walk is a quite complicate and state of the art issue. The simplest random walk is given below, some people call it "the drunken man":
Where X(t) is the random walk, a variable that can take values depending on previous values and previous random contributions.
This process is called Brownian motion and it was studied by Robert Brown in 1827, later studied mathematically and physically by Einstein, Bachelier e others. They have developed the diffusion theory, which is the most well-know random walk.
Suppose:
So, for our simple model:
The relation was obtained by using the property that if two variable are independent, you can sum their expected values, and the expected value of a constant is the constant.
A more complex process is possible, see:
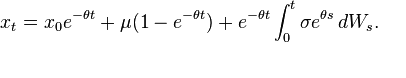
and mean value:
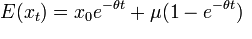
See for a simulation on random walk:
https://en.wikipedia.org/wiki/Brownian_motion
See for more details in the previously mentioned random process:
https://en.wikipedia.org/wiki/Ornstein%E2%80%93Uhlenbeck_process

