How do you evaluate #((8), (5))# using Pascal's triangle?
2 Answers
Feb 26, 2017
Explanation:
Feb 26, 2017
Explanation:
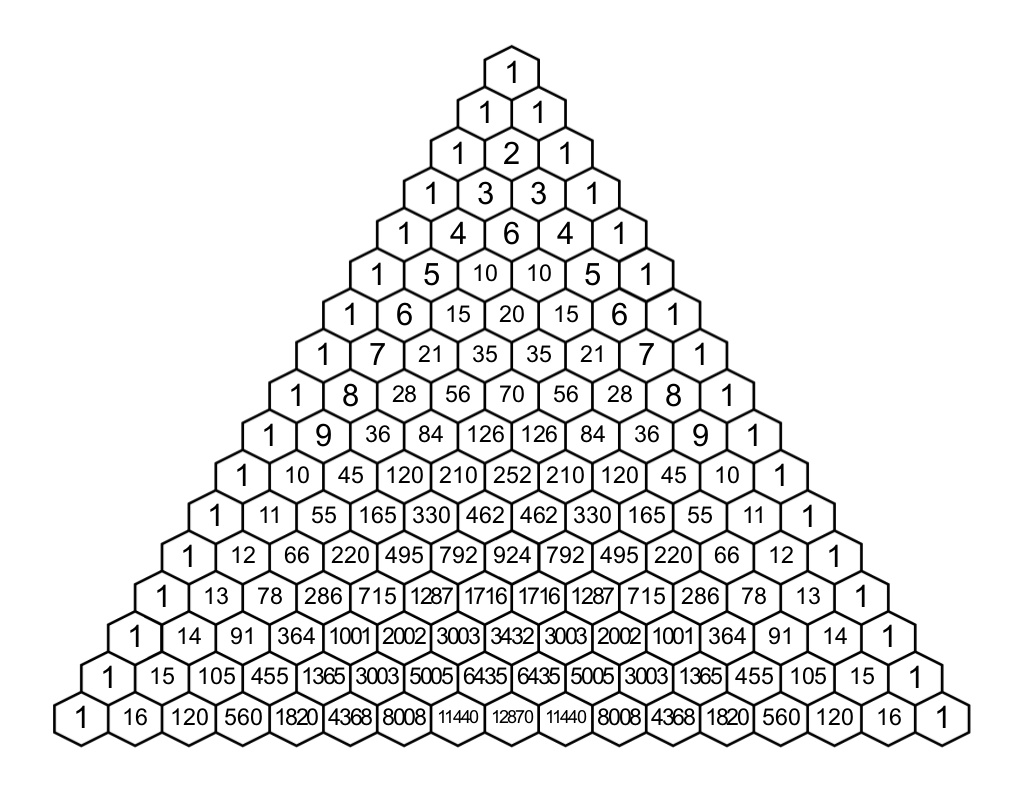
#((8),(5))" represents 8th row , 5th column"# From Pascal's triangle the entry in the 8th row / 5th column is
#((8),(5))=56#
#"8th row "rarr1 color(white)(x)8color(white)(x) 28color(white)(x) 56color(white)() color(white)(x)70color(white)(x)color(red)(56)color(white)(x)28color(white)(x)8color(white)(x)1#
#color(white)(xxxxxxxxxxxxxxxxxxx)uarr#
#color(white)(xxxxxxxxxxxxxxxxxx)"5th column"#

