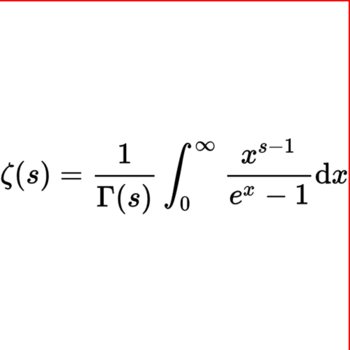Question

How do you evaluate `\sqrt { 777924} - \sqrt { \sqrt { 31696} } - \sqrt { 30+ \sqrt { 1156} } + \sqrt { 4624}`?

Answer 1

`942 - 2\root{4}{1981} ~= 928.657`

Explanation:

I rather use one of "Prime Factorization Calculator" like this one, you can do it yourself but I think it wastes your time.
Let's do it:
`777924 = 2^2*3^4*7^4 => \sqrt(777924) = 2*3^2*7^2 = 882`

`31696 = 2^4*7*283 => \sqrt(\sqrt(31696)) = 2\sqrt(\sqrt(7*283))`

`31696 = 2^4*7*283 => \sqrt(\sqrt(31696)) = 2\sqrt(\sqrt(7*283)) = 2\root{4}{1981}`

`1156 = 2^2*17^2 => \sqrt(1156) = 2*17=34 => \sqrt(30+\sqrt(1156)) = \sqrt(64) = 8`

`4624 = 2^4*17^2 => \sqrt(4624) = 2^2*17 = 68`

and answer will be:

`882 - 2\root{4}{1981} - 8 + 68`
`942 - 2\root{4}{1981} ~= 928.657`