Question

How do you evaluate `x( 5x - 4) ( 2x - 3)`?

Answer 1

`10x^3 - 23x^2 + 12x`

Explanation:

First, use the distributive property (shown below) to simplify `x(5x-4)`:

Following this image, we know that:
`color(blue)(x(5x-4)) = (x * 5x) + (x * -4) = 5x^2 - 4x`

Put that back into the expression:
`(5x^2 - 4x)(2x-3)`

Now use the distributive method FOIL (shown below) to simplify the rest of the expression:

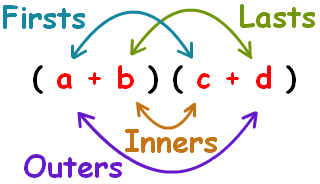
Following this image, we can multiply it out.

The `color(teal)("firsts")`:
`color(teal)(5x^2 * 2x) = 10x^3`

The `color(indigo)("outers")`:
`color(indigo)(5x^2 * -3) = -15x^2`

The `color(peru)"inners"`:
`color(peru)(-4x * 2x) = -8x^2`

The `color(olivedrab)"lasts"`:
`color(olivedrab)(-4x * -3) = 12x`

Combine them all together to get:
`10x^3 - 15x^2 - 8x^2 + 12x`

We can still combine the like terms `color(blue)(-15x^2)` and `color(blue)(-8x^2)`:
`10x^3 - 23x^2 + 12x`

Hope this helps!

Answer 2

`10x^3-23x^2+12x`

Explanation:

`x(5x-4)(2x-3)=x(10x^2-8x-15x+12)`
`x(10x^2-23x+12)=10x^3-23x^2+12x`