Question

How do you express the complex number in trigonometric form 2i?

Answer 1

I found: `z=2(cos(pi/2)+isin(pi/2))`

Explanation:

If you plot this complex number on the complex plane you'll see it as:

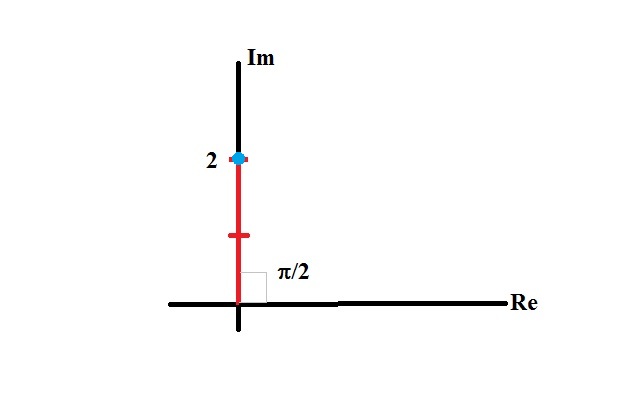
It has a modulus (length) of `2` and argument (angle with positive Re semiaxis) of `pi/2`.
So in trigonometric form your number will be:
`z=2i=2(cos(pi/2)+isin(pi/2))`