How do you find a power series representation for (x-2)^n/(n^2) and what is the radius of convergence?
1 Answer
Explanation:
Suppose that our quest is for
In this case a variable change
In the next steps we will try to build such a power series.
We begin with
This power series is convergent for
now integrating
The last step is covered by integrating
or equivalently
The description of function PolyLog can be found in
https://en.wikipedia.org/wiki/Polylogarithm
The convergence interval in
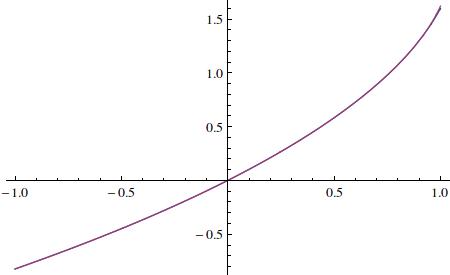
The attached figure shows the agreement between