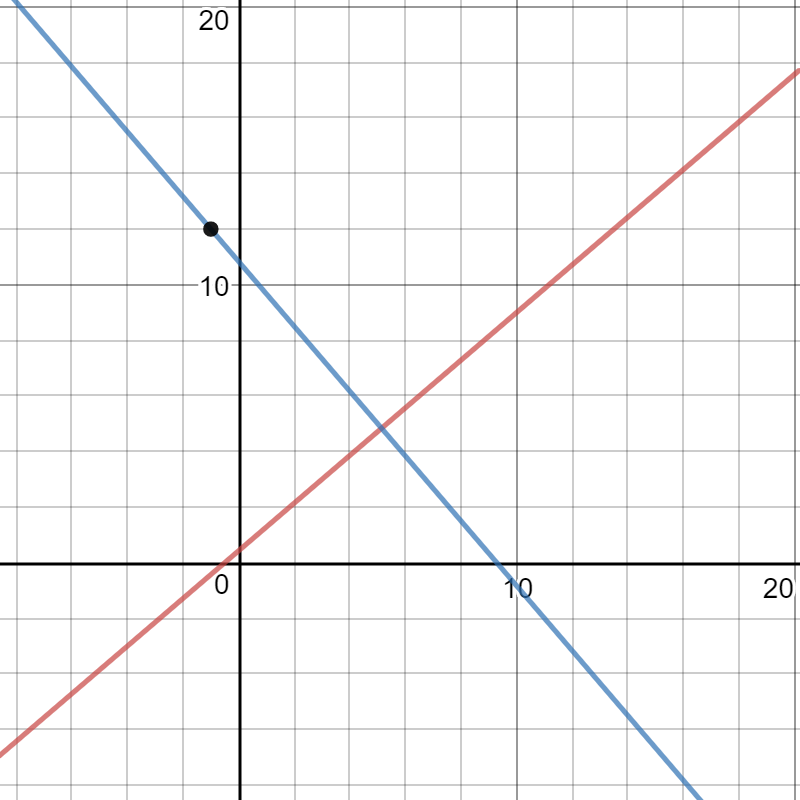
How do you find a standard form equation for the line with point (-1,12) and is perpendicular to the line is , where 6x - 7y + 3 = 0?

Question

1021 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-12-05T17:33:52

When given the equation of a line in the standard form,

#Ax + By = C#

you obtain the standard equation form of all lines that are perpendicular by swapping A and B and change the sign of one.

Given:

#6x - 7y = -3#

Please observe that #A = 6# and #B = -7#

To make the standard form of all lines that are perpendicular, swap A and B and, because B is negative, I shall change the sign of B:

#7x +6y = D#

To find the value of D, evaluate the standard from at the given point, #(-1,12)#:

#7(-1) +6(12) = D#

#D = 65#

The standard form of the equation of the desired line is:

#7x +6y = 65#

Here is an image with, #6x - 7y = -3# in red, #7x +6y = 65# in blue, and #(-1,12)# in black:

www.desmos.com/calculator