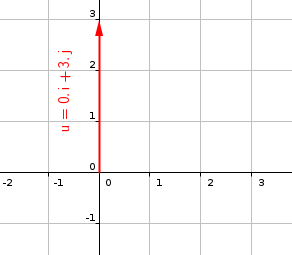
#"the vector u is shown in figure below"#
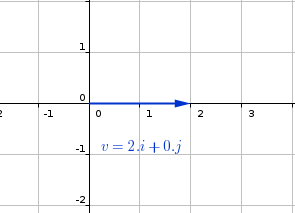
#"the vector v is shown in the diagram below"#
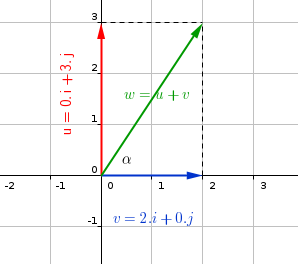
#"a)the vector w=u+v is shown in the diagram below"#
#w=2.i+3.j#
#"magnitude of w can be calculated :"#
#w=sqrt(2^2+3^2)#
#w=sqrt(4+9)" , "w=sqrt(13)#
#"direction of the vector w is"#
#tan alpha=3/2#
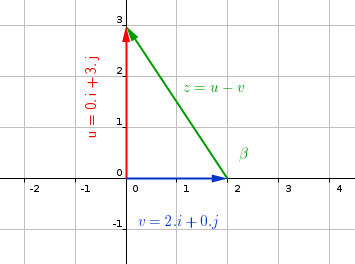
#"a)the vector z=u-v is shown in the diagram below"#
#z=-2.i+3.j#
#"magnitude of z can be calculated :"#
#w=sqrt((-2)^2+3^2)#
#w=sqrt(4+9)" , "w=sqrt(13)#
#"direction of the vector w is"#
#tan beta=-3/2#
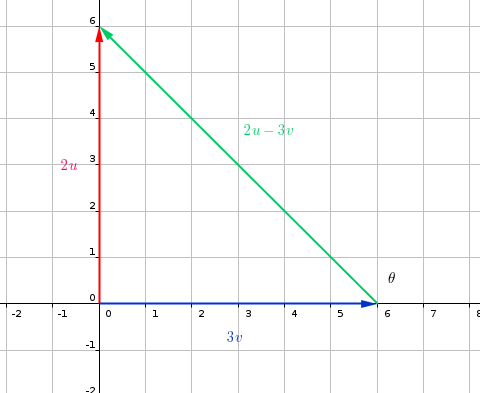
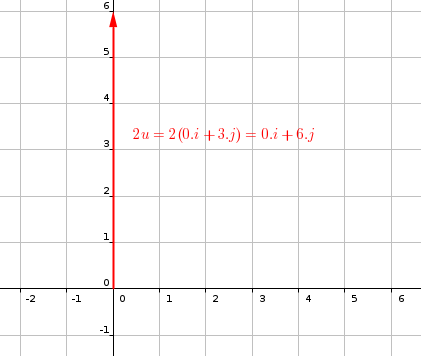
#c)"The vector 2u is shown in the figure below"#
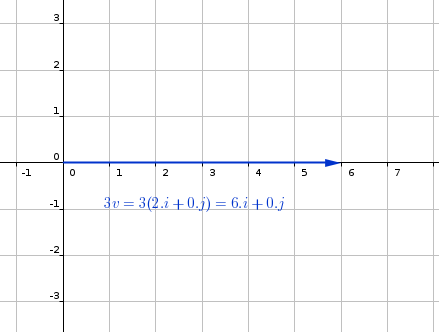
#"The vector 3v is shown in the figure below"#
#"p=2u-3v is shown in the figure below"#
#"magnitude of p can be calculated :"#
#p=sqrt((-6)^2+6^2)#
#p=sqrt(36+36)" , "p=sqrt(72)=6sqrt(2)#
#"direction of the vector p is"#
#tan theta=-6/6#=-1