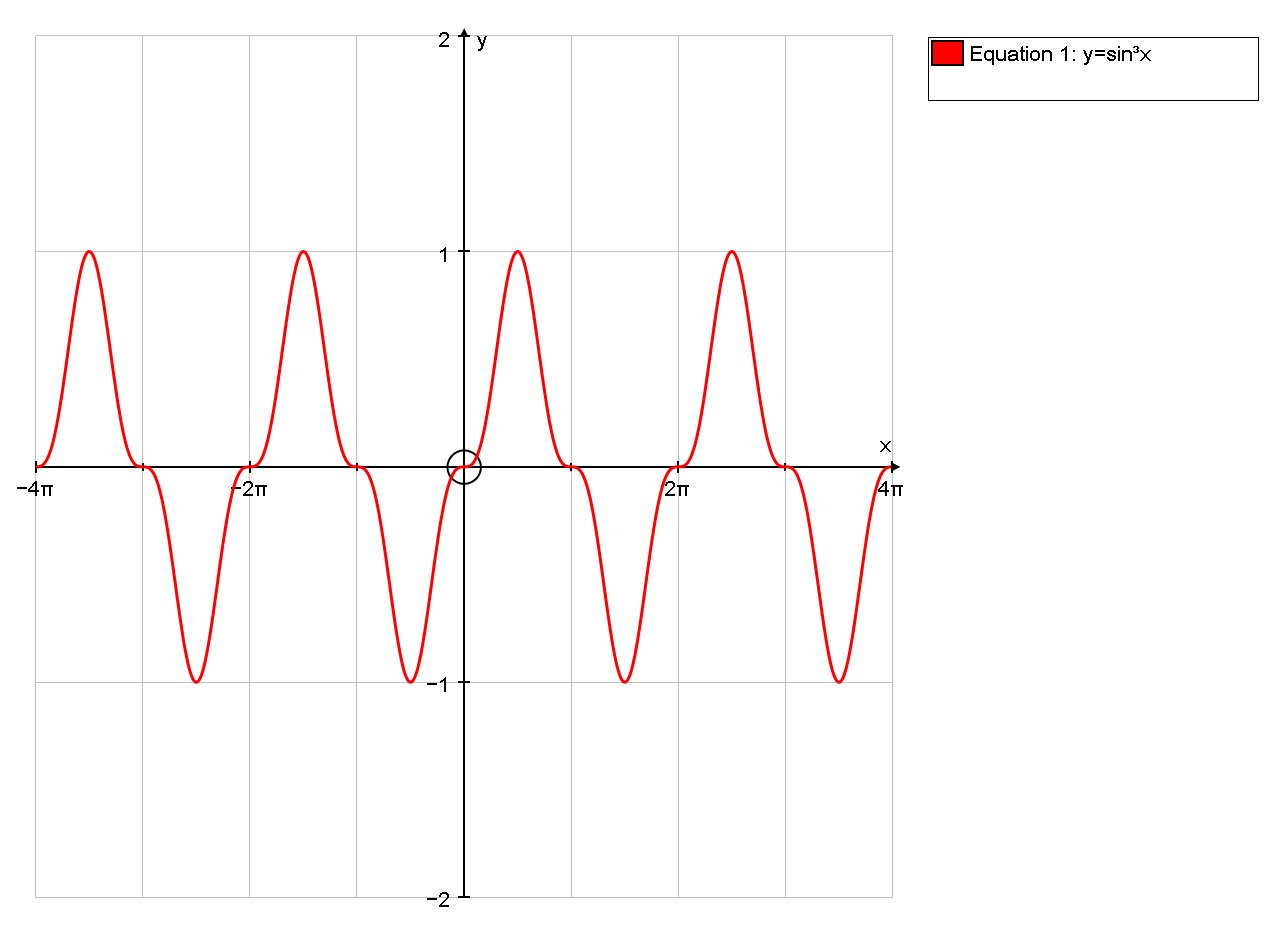
We have # y =sin^3x # .... [1]
We first find the max/min critical points by finding values of #x# such that #dy/dx=0#
Differentiating [1] wrt #x# using the chain rule we get:
# dy/dx = 3sin^2xcosx # .... [2]
# dy/dx = 0 => 3sin^2xcosx = 0#
# :. sin^2xcosx = 0#
# :. sin^2x = 0 # or #cosx = 0#
If # sin^2x = 0 => sin x =0 => x=npi, n in ZZ #
And #cosx = 0 => x=npi-pi/2, n in ZZ #
To determine the nature of these points we need to look at the second derivative
Differentiating [2] wrt [x] and simultaneously applying the chain rule and product rule we have;
# (d^2y)/dx^2 = (3sin^2x)(-sinx) + (6sinxcosx)(cosx) #
# :. (d^2y)/dx^2 = 6sinxcos^2x - 3sin^3x #
We already know that min/max occurs when #x=npi# or# x=npi-pi/2#, so let's find # (d^2y)/dx^2# at these points;
When # x=npi => (d^2y)/dx^2 = 6(0)cos^2x - 3(0) = 0 #
So we can conclude that # x=npi # correspond to points of inflexion
When # x=npi-pi/2 => (d^2y)/dx^2 = 6sinx(0) - 3sin^3(npi-pi/2) #
# :. (d^2y)/dx^2 = - 3sin^3(npi-pi/2) # .... [3]
Now # sin(A-B) -= sinAcosB - cosAsinB #
# :. sin(npi-pi/2) = sinnpicos(pi/2) - cos npi sin (pi/2) #
# :. sin(npi-pi/2) = (sinnpi)(0) - cos npi (1) #
# :. sin(npi-pi/2) = - cos npi #
And so, substituting into [3] gives us:
# :. (d^2y)/dx^2 = - 3(- cos npi)^3 #
# :. (d^2y)/dx^2 = 3cos^3 npi #
So we can conclude that
# { ((d^2y)/dx^2 <0, n " odd",=>, "maximum"), ((d^2y)/dx^2>0, n " even", =>, "minimum") :} #
So Points of Inflection occur when #x=npi#,
ie #x=-3pi,-2pi,-pi,0,pi,2pi,3pi, ... #
Maximum points occur when #x=npi-pi/2# and n is odd
ie #x=(-11pi)/2,(-7pi)/2,(-3pi)/2,pi/2, (5pi)/2, (9pi)/2, ...#
Minimum points occur when #x=npi-pi/2# and n is even
#x=(-9pi)/2,(-5pi)/2,(-pi/2), (3pi)/2,(7pi)/2, ...#
This can be visualised by the graph