Question

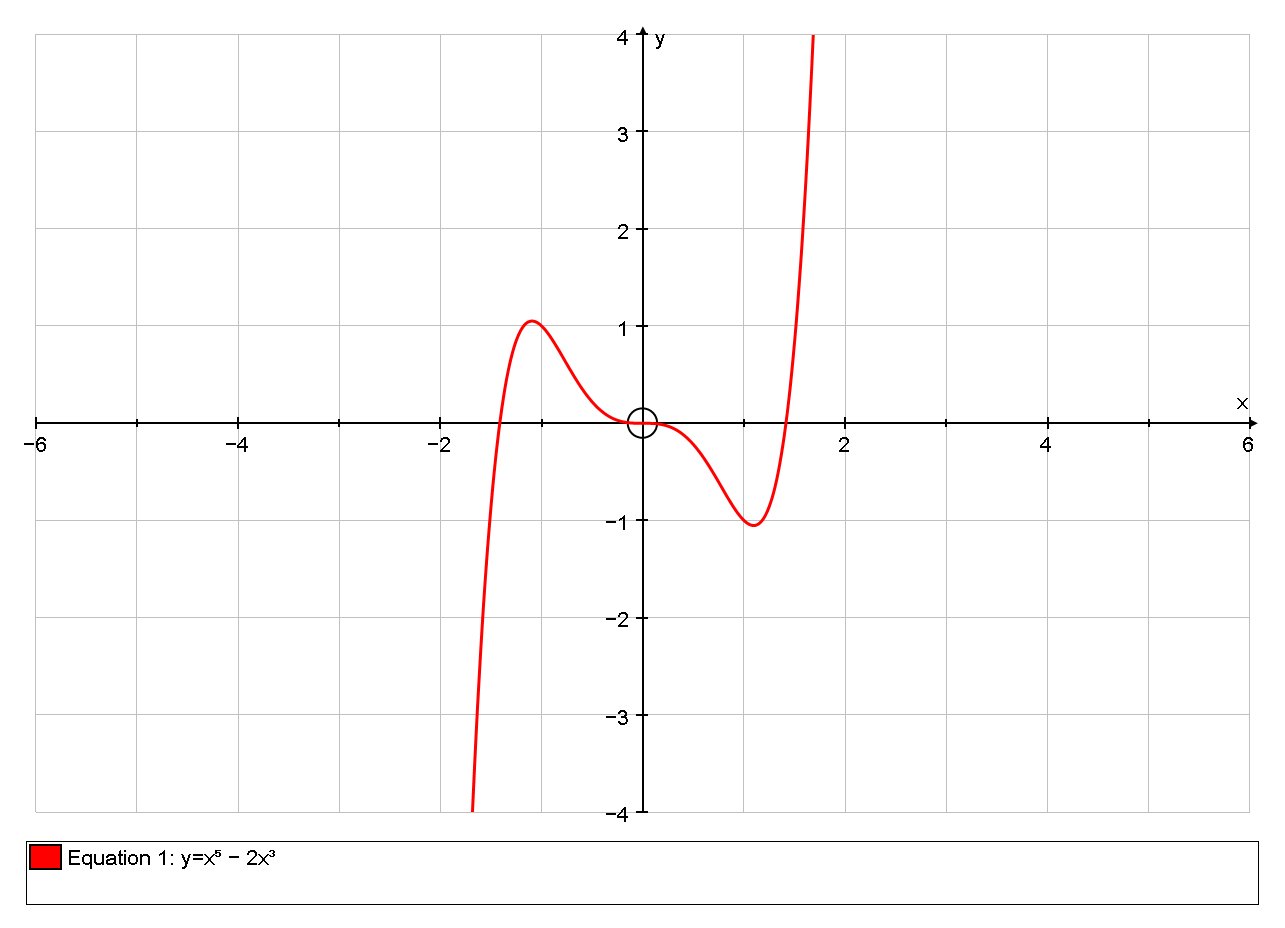
How do you find all points of inflection given `y=x^5-2x^3`?

Answer 1

There is just one point of inflection at the origin

Explanation:

`y = x^5 - 2x^3`

Differentiating wrt `x` we have'

`dy/dx = 5x^4 - 6x^2`

At a critical point , `dy/dx = 0`
`dy/dx = 0 => 5x^4 - 6x^2 = 0`
`:. x^2(5x^2 - 6) = 0`
So, Either `x^2 = 0 => x= 0`, or `5x^2 - 6 = 0 => x =+- sqrt(6/5)`

So critical points occurs when `x=0, x =+- sqrt(6/5)`

Next we can find the nature of th critical points by looking at the second derivative:

`dy/dx = 5x^4 - 6x^2`
`:. (d^2y)/(dx^2) = 20x^3 - 12x`
`:. (d^2y)/(dx^2) = 4x(5x^2 - 3)`

When # { (x=-sqrt(6/5), => (d^2y)/(dx^2)<0,=>,"maximum"), (x=0, => (d^2y)/(dx^2)=0,=>,"inflection"), (x =sqrt(6/5), => (d^2y)/(dx^2)>0,=>,"minimum") :} #

So therei is one point of inflection when `x=0 => y=0`