Question

How do you find an equation of the tangent line to the curve at the given point `y=e^(2x) cos (pix)` and `(0,1)`?

Answer 1

Compute the first derivative.
The slope is the first derivative evaluated at the x coordinate.
Use the point-slope form of the equation of a line.

Explanation:

Compute the first derivative:

`dy/dx = e^(2x)(2cos(pix)-pisin(pix))`

The slope at the point of tangency is the first derivative at evaluated at the x coordinate, `x = 0`:

`m = e^(2(0))(2cos(pi(0))-pisin(pi(0)))`

`m = 2`

Use the point-slope form of the equation of a line:

`y = m(x-x_1)+y_1`

Where `(x_1,y_1) = (0,1)`:

NOTE: Because the given point happens to be the y-intercept we could have used the slope-intercept form but I thought it better to use the more general case.

`y = 2(x-0)+1`

`y = 2x+1 larr` here is the equation of the tangent line.

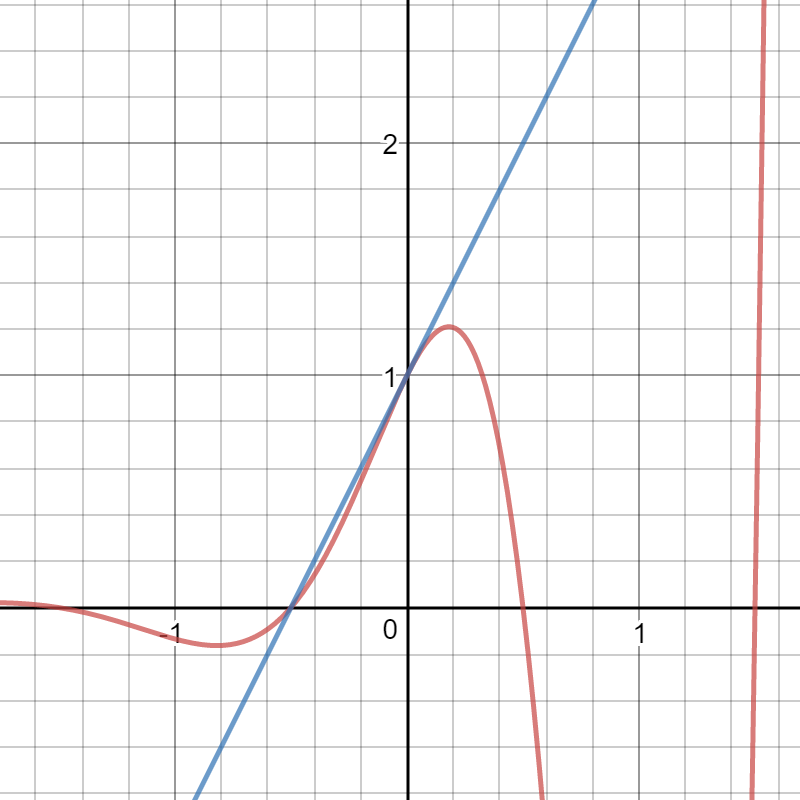
Here is a graph of both the function and the tangent line: