How do you find and classify all the critical points and then use the second derivative to check your results given #y=x^2+10x-11#?
1 Answer
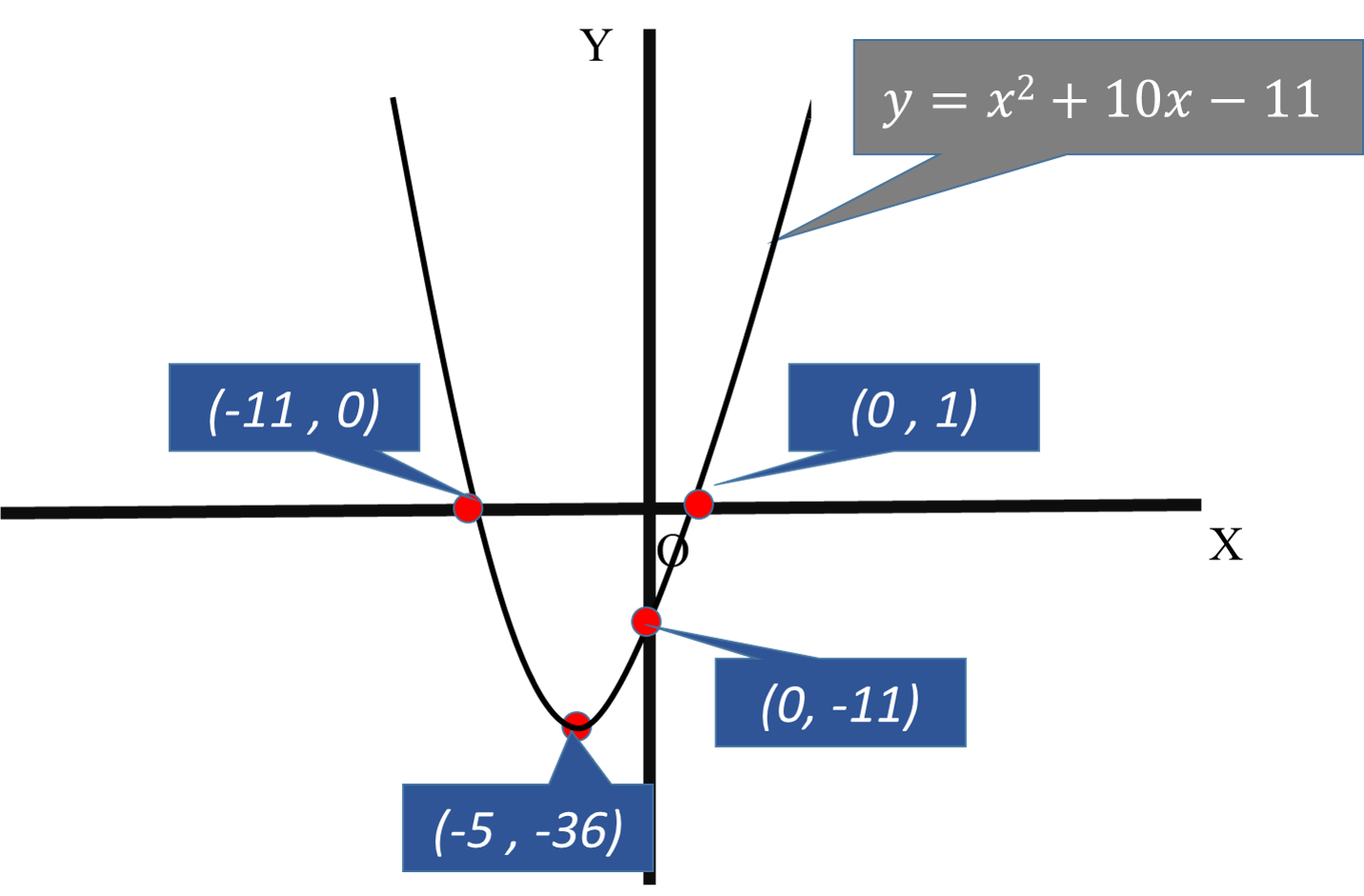
Vertex
Y-intercept
X-intercepts
Explanation:
Given -
#y=x^2+10x-11#
It is a quadratic equation .
It has only one critical point.
It is the vertex.
#x=(-b)/(2a)=(-10)/(2 xx 1)=-5#
At
#y= 25-50-11=25-61=-36#
Vertex is
Derivatives of the function are
#dy/dx=2x+10#
#(d^2y)/(dx^2)=2 > 0#
Its second derivative is greater than zero. The curve is concave upwards.
Its other important points are
Y-intercept
At
At
X- intercepts
At
# x^2+11x-x-11=0#
#x( x+11)-1(x+11)=0#
#(x+11)(x-1)=0#
#x+11=0#
#x=-11#
#x-1=0#
#x=1#
At points