Question

How do you find general form of circle with Center at the point (1, 0) and having the point (-2, 3)?

Answer 1

`(x-1)^2+y^2=18`

Explanation:

The general form for a circle with center `(a,b)` and radius `r` is
`color(white)("XXX")(x-a)^2+(y-b)^2 = r^2`

If the center of the circle is at `(x_c,y_c)=(1,0)`
and
`(x_p,y_p)=(-2,3)` is a point on the circle, then the radius squared is
`color(white)("XXX")r^2 = (x_p-x_c)^2+(y_p-y_c)^2color(white)("XXX")`(Pythagorean Theorem)

`color(white)("XXXX")=(-2-1)^2+(3-0)^2 = 3^2+3^2 = 9+9 = 18`

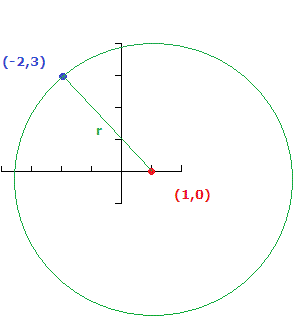
Combining this information concerning the radius (squared)
and the general form for a circle, we get
`color(white)("XXX")(x-1)^2+(y-0)^2=18`