Question

How do you find general form of circle with center at the point (5,7); tangent to the x-axis?

Answer 1

`(y-7)^2 + (x-5)^2 = 49`

Explanation:

The general form of a circle is `(y-k)^2 +(x-h)^2 = r^2`
where `(h,k)` is the centre of the circle and `r` is the radius.

Because the circle is tangent to the `x` axis and the `y` coordinate of the centre is `7`, the radius `r = 7` - see sketch.

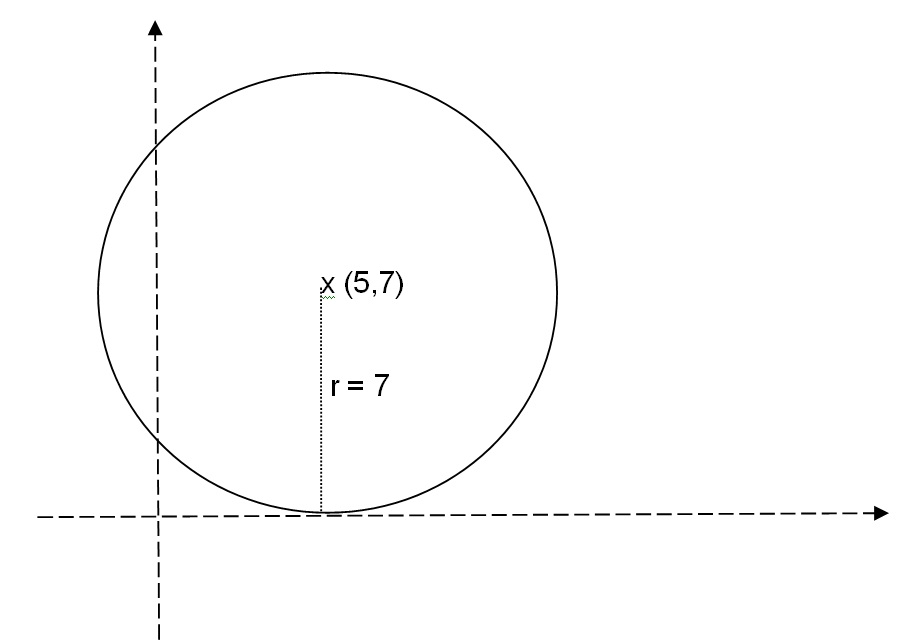
So the equation becomes
`(y-7)^2 + (x-5)^2 = 7^2`

`(y-7)^2 + (x-5)^2 = 49`