How do you find #lim (1+5/sqrtu)/(2+1/sqrtu)# as #u->0^+# using l'Hospital's Rule?
2 Answers
May 5, 2017
5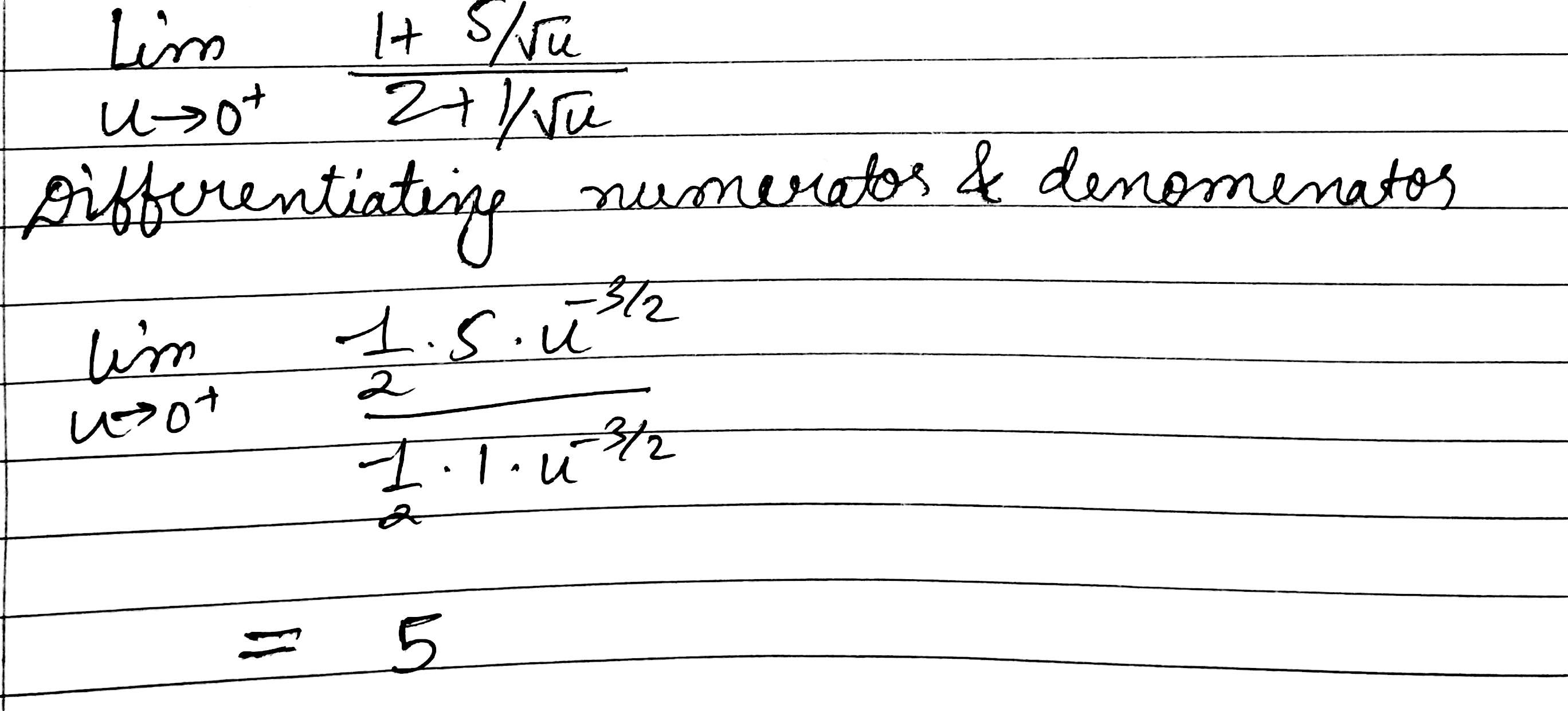
May 5, 2017
# lim_(u rarr 0^+) (1+5/sqrt(u))/(2+1/sqrt(u)) = 5 #
Explanation:
We do not need to apply L'Hôpital's as this is a trivial limit to evaluate:
# lim_(u rarr 0^+) (1+5/sqrt(u))/(2+1/sqrt(u)) = lim_(u rarr 0^+) (1+5/sqrt(u))/(2+1/sqrt(u))*sqrt(u)/sqrt(u) #
# " " = lim_(u rarr 0^+) (sqrt(u)+5)/(2sqrt(u)+1) #
# " " = 5/1 #
Note that the above limit is only valid for
# u rarr 0^+ => u > 0 => sqrt(u) in RR #
Whereas:
# u rarr 0^- => u < 0 => sqrt(u) in CC #


