How do you find local maximum value of f using the first and second derivative tests: #f(x) = x^(3) - 6x^(2) + 5#?
1 Answer
The local maximum value of the function is
Explanation:
There are two ways local extrema (minima and maxima) can be determined--the first and second derivative tests. Both find the same things, using slightly different (yet both valid) methods.
Finding Critical Values
Before launching into the tests, it's first necessary to identify any critical values of the function that may exist.
A critical value exists at
To find the critical values of the given function, differentiate it.
#f'(x)=3x^2-12x#
A critical value could occur when
#3x^2-12x=0#
Dividing every term by
#x^2-4x=0#
#x(x-4)=0#
Therefore we have two critical values:
First Derivative Test
The first derivative test involves looking at the derivative of a function directly surrounding a critical value.
Since at these critical values the derivative equals
The first derivative test uses the way these extrema work to determine whether an extremum is a relative minimum, maximum, or neither.
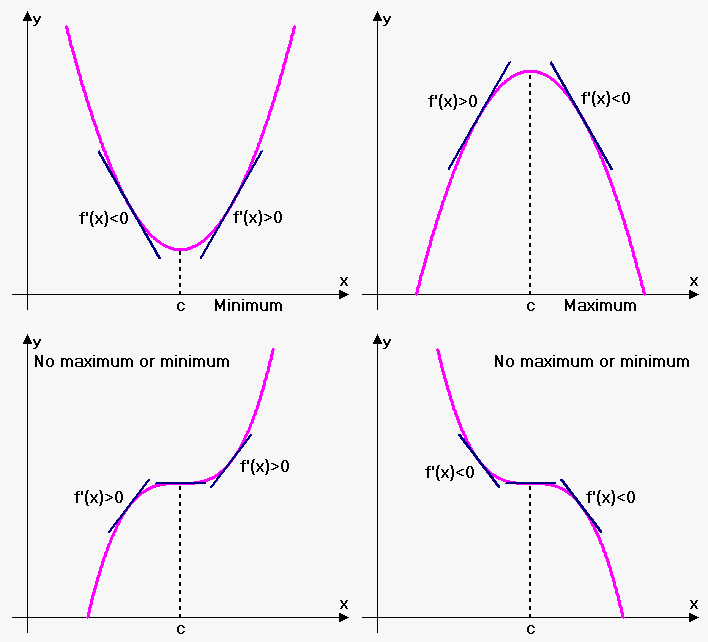
As the picture depicts, when there is a relative minimum, the graph will make a
A relative maximum works in reverse: to the left, the function is increasing, so its derivative is positive, and to the right, the function is decreasing, so its derivative is negative.
There also exist cases in which the derivative to either side of the critical point does not change sign--this is indicative of a "saddle point," where there is not an extremum yet the graph momentarily flattens and has a horizontal tangent.
So, our game plan should be to take our two critical values,
Around
#f'(-1)=3(-1)^2-12(-1)=3+12=15# Since this is positive, the function is increasing to the left of the critical value at
#x=0# .
#f'(1)=3(1)^2-12(1)=3-12=-9# Since this is negative, the function is decreasing to the right of the critical value at
#x=0# .Since the function goes from increasing, to flattening out at
#x=0# , then decreasing,#x=0# is a relative maximum.
Since we're dealing with a cubic equation, we can intuit that the other critical value will be a relative minimum, but we should check this to be thorough.
Checking the sign of the derivative around
#f'(3)=3(3)^2-12(3)=27-36=-9# This is negative--the function is decreasing to the left of the critical value.
#f'(5)=3(5)^2-12(5)=75-60=15# The function is increasing to the right of the critical value.
Indeed, since the function went from decreasing to increasing around
#x=4# , there is a relative minimum at#x=4# .
Second Derivative Test
This method, of course, will use the second derivative, so we should go ahead and differentiate the first derivative:
#f''(x)=6x-12#
The second derivative uses the concavity at a critical value to determine what type of extremum exists there.

The two concavities are displayed above. Notice that the concave down shape always produces a maximum, while the concave up shape will always produce a minimum.
Thus, if the second derivative is positive at a critical value, the function is concave up there and there exists a relative minimum at the critical value. Similarly, if the second derivative is negative at the critical value, the function is concave down and there is a relative maximum at the critical value.
Test both critical values in the second derivative:
#f''(0)=6(0)-12=0-12=-12# Since this is negative, the function is concave down at
#x=0# , so#x=0# must be a relative maximum.
#f''(4)=6(4)-12=24-12=12# Since this is positive, the function is concave up at
#x=4# , so#x=4# must be the location of a relative minimum.
Note that the first and second derivative tests yielded the same results, just in a different way. It's really your choice as to which to use--the first derivative test only requires you to differentiate a function once, but after finding critical values, you have to use a large number of test points which can be cumbersome. For the second derivative test, you have to differentiate the function twice, which may be laborious for more difficult functions, but it doesn't require testing of nearly as many points.
Important Reminder
Note that the question asked for "the local maximum value" of the function.
We determined that the location of the local maximum was at
To find the maximum value, simply find the function value at
#f(0)=(0)^3-6(0)^2+5=5#
The local maximum value of the function is

