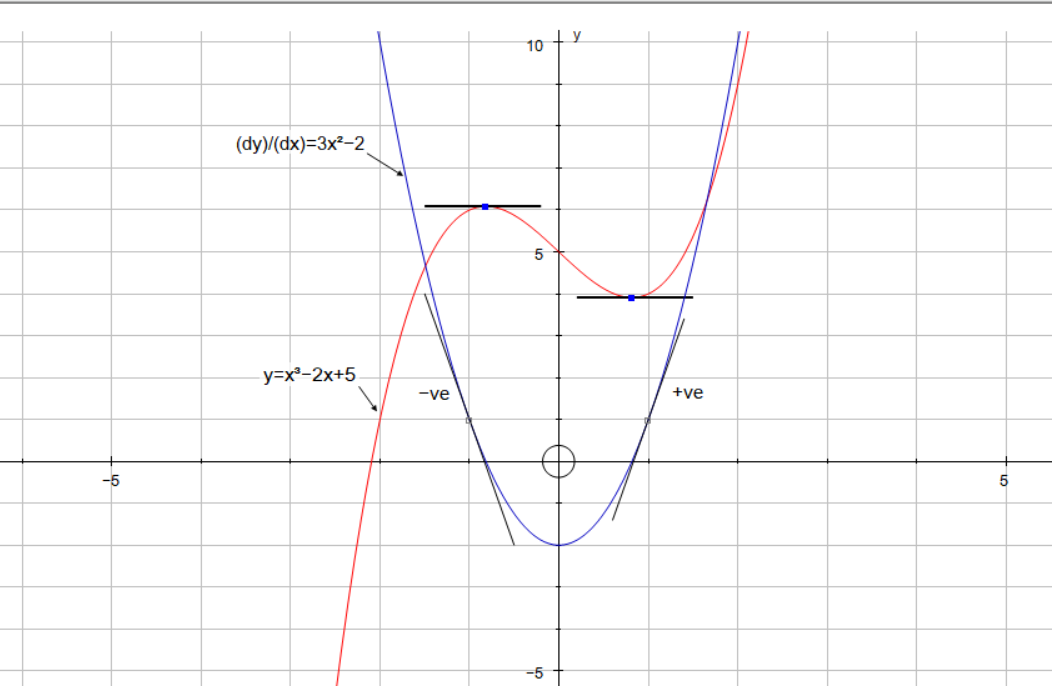
How do you find local maximum value of f using the first and second derivative tests: #f(x)=x^3-2x+5# on the interval (-2,2)?

Question

3745 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-11-27T22:04:44

See below.

First differentiate #x^3-2x+5#

#d/dx(x^3-2x+5)=3x^2-2#

equating this to zero and solving fot #x# will give us the points where the tangent is horizontal .i.e. maximum and minimum values.

#3x^2-2=0=>x= +-sqrt(2/3)#

We now use the second derivative test. If:

#(d^2y)/(dx^2)>0# minimum value.

#(d^2y)/(dx^2)<0# maximum value.

#(d^2y)/(dx^2)=0# min/max or point of inflection.

Second derivative:

#(d^2y)/(dx^2)(3x^2-2)=6x#

#6(+sqrt(2/3))>0# min value.

#6(-sqrt(2/3))<0# max value.

These are both in the interval #( -2 , 2 )#

#x=-sqrt(2/3)# give maximum value so:

#f(-sqrt(2/3))=(-sqrt(2/3))^3-2(-sqrt(2/3))+5#

#->=(4sqrt(6))/9+5~~6.089#

Graph of function and first derivative:

enter image source here