How do you find the 95% confidence interval?
Find the 95% confidence interval for a sample of size 39 with a mean of 20.3 and a standard deviation of 10.2.
Find the 95% confidence interval for a sample of size 39 with a mean of 20.3 and a standard deviation of 10.2.
1 Answer
A 95% confidence interval with the given data gives:
Explanation:
The confidence interval is given by the formula:
Or you can write it as:
Where
We know all the values except for
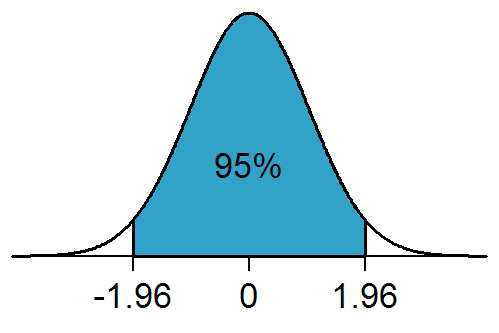
As you can see from this picture the
I hope you can see that to the left and right of the shaded area, 2.5% is taken up by the white space each side.
So therefore you do 95%+2.5% = 97.5% then you can look that value up in the tables which is in fact: 1.96.
Now you can just substitute all the numbers into the expression:
Enter this into your calculator and you get:
Hope this helps!


