Question

How do you find the arc length of the curve `y = sqrt( 2 − x^2 )`, `0 ≤ x ≤ 1`?

Answer 1

I found: `s=sqrt(2)pi/4=1.11`

Explanation:

I plotted the arc you need (a bit of a cirle) and found:

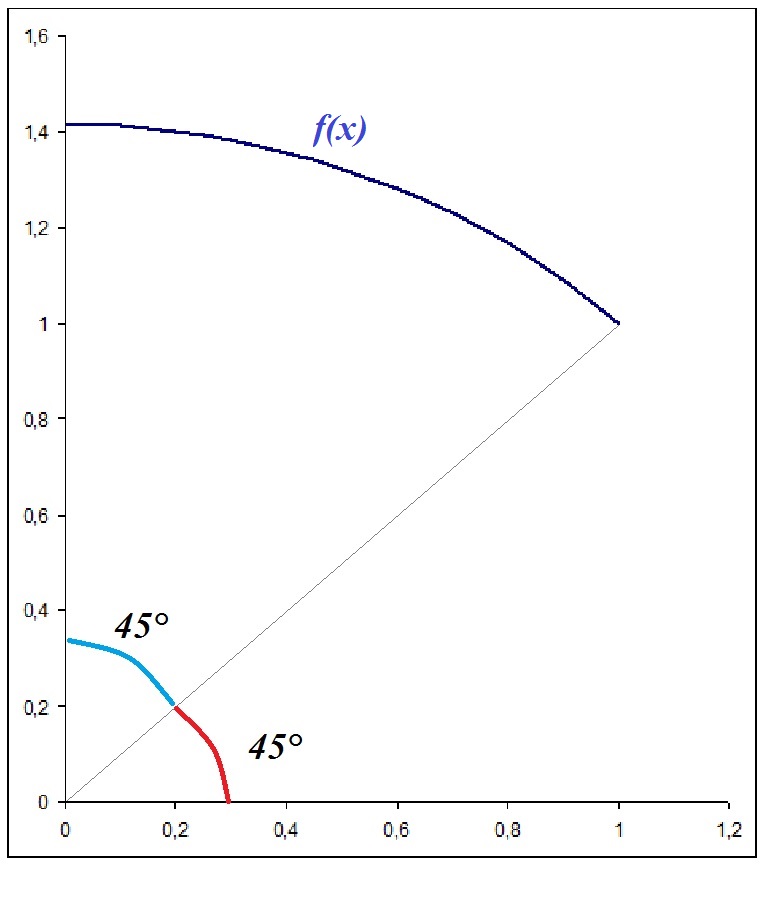
The arc length `s` is given as:
`s=r*theta`
where `r=sqrt(2)` is the radius (obtained setting `x=0` into the function) and `theta=45°=pi/4` is the angle (we need to use radians). So you get that:
`s=sqrt(2)pi/4=1.11`